题目内容
已知关于x的方程sinx+
cosx-a=0有实数解,则实数a的取值范围是( )
| 3 |
| A、[-2,2] | ||||
| B、(-2,2) | ||||
| C、[-1,1] | ||||
D、[-1-
|
考点:两角和与差的正弦函数
专题:计算题,函数的性质及应用,三角函数的图像与性质
分析:关于x的方程sinx+
cosx-a=0有解,即a=sinx+
cosx=2sin(x+
)有解,结合正弦函数的值域可得a的范围.
| 3 |
| 3 |
| π |
| 3 |
解答:
解:关于x的方程sinx+
cosx-a=0有解,
即a=sinx+
cosx=2sin(x+
)有解,
由于x为实数,则2sin(x+
)∈[-2,2],
故有-2≤a≤2,
故选A.
| 3 |
即a=sinx+
| 3 |
| π |
| 3 |
由于x为实数,则2sin(x+
| π |
| 3 |
故有-2≤a≤2,
故选A.
点评:本题主要考查两角和差的正弦公式、正弦函数的值域,属于中档题.

练习册系列答案
相关题目
设x>0,y>0,x+y=1,则
+
≤a恒成立的a的最小值是( )
| x |
| y |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、2
|
甲、乙、丙、丁、戊和己6名学生进行劳动技术比赛,决出第一到第六名的名次.甲、乙两名参赛者去询问成绩,回答者对甲说“很遗憾,你和乙都没有得到冠军”,对乙说“你当然不会是最差的”.从上述回答分析,6人的名次排列可能有( )种不同情况.
| A、180 | B、288 |
| C、384 | D、480 |
一物体的运动方程为S=6t2+3t-2,则它在t=3时的瞬时速度为( )
| A、36 | B、39 | C、12 | D、33 |
已知函数f(x)=x2,则下列各式中正确的是( )
| A、f(-1)>f(2)>f(-3) |
| B、f(2)>f(-1)>f(-3) |
| C、f(-3)>f(2)>f(-1) |
| D、f(-3)>f(-1)>f(2) |
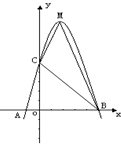 已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(-1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.
已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(-1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.