题目内容
20.一竖立在地面上的圆锥形物体的母线长为4m,侧面展开图的圆心角为$\frac{2π}{3}$,则这个圆锥的体积等于( )| A. | $\frac{\sqrt{15}}{3}$πm3 | B. | $\frac{32\sqrt{35}}{27}$πm3 | C. | $\frac{32\sqrt{35}}{81}$πm3 | D. | $\frac{128\sqrt{2}}{81}$πm3 |
分析 根据已知求出圆锥的底面半径和高,代入圆锥体积公式,可得答案.
解答 解:设圆锥的底面半径为r,
圆锥形物体的母线长l=4m,侧面展开图的圆心角为$\frac{2π}{3}$,
故2πr=$\frac{2π}{3}$l,
解得:r=$\frac{4}{3}$m,
故圆锥的高h=$\sqrt{{l}^{2}-{r}^{2}}$=$\frac{8}{3}\sqrt{2}$m,
故圆锥的体积V=$\frac{1}{3}{πr}^{2}h$=$\frac{128\sqrt{2}}{81}$πm3,
故选:D
点评 本题考查的知识点是旋转体,熟练掌握圆锥的几何特征和体积公式是解答的关键.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
12.若方程2x=2-2x恰有一个实数根x0,则x0所在的区间是( )
| A. | (0,$\frac{1}{4}$) | B. | ($\frac{1}{4}$,$\frac{1}{2}$) | C. | ($\frac{1}{2}$,$\frac{3}{4}$) | D. | ($\frac{3}{4}$,1) |
9.定义在区间(0,+∞)上的函数f(x)>0,且f(x)<xf′(x)<2f(x)恒成立,其中f′(x)为f(x)的导函数,则( )
| A. | $\frac{1}{8}$<$\frac{f(1)}{f(2)}$<$\frac{1}{4}$ | B. | $\frac{1}{4}$<$\frac{f(1)}{f(2)}$<$\frac{1}{2}$ | C. | $\frac{1}{2}$<$\frac{f(1)}{f(2)}$<1 | D. | $\frac{1}{3}$<$\frac{f(1)}{f(2)}$<$\frac{1}{2}$ |
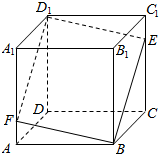 如图所示,在正方体ABCD-A1B1C1D1中,点E是棱CC1上的一个动点,平面BED1交棱AA1于点F.则下列命题中真命题的个数是( )
如图所示,在正方体ABCD-A1B1C1D1中,点E是棱CC1上的一个动点,平面BED1交棱AA1于点F.则下列命题中真命题的个数是( )