题目内容
8.已知$\overrightarrow{a}$=(2cosα,2sinα),$\overrightarrow{b}$=(cosβ,sinβ),0<α<β<2π,设$\overrightarrow{c}$=(2,0),若$\overrightarrow{a}$+2$\overrightarrow{b}$=$\overrightarrow{c}$,求α+β的值.分析 $\overrightarrow{a}$+2$\overrightarrow{b}$=$\overrightarrow{c}$,利用向量坐标运算及其相等可得:cosα+cosβ=1,sinα+sinβ=0,利用cos2β+sin2β=(1-cosα)2+sin2α=1-2cosα+1=1,化为cosα=$\frac{1}{2}$,由于0<α<β<2π,可得α=$\frac{π}{3}$或$\frac{5π}{3}$.分类讨论即可得出.
解答 解:∵$\overrightarrow{a}$+2$\overrightarrow{b}$=$\overrightarrow{c}$,
∴(2cosα,2sinα)+2(cosβ,sinβ)=(2,0),
∴2cosα+2cosβ=2,2sinα+2sinβ=0,
分别化为:cosα+cosβ=1,sinα+sinβ=0,
∵cos2β+sin2β=(1-cosα)2+sin2α=1-2cosα+1=1,
化为cosα=$\frac{1}{2}$,
∵0<α<β<2π,
∴α=$\frac{π}{3}$或$\frac{5π}{3}$.
∵sinα+sinβ=0,
∴当α=$\frac{π}{3}$时,β=$\frac{4π}{3}$或$\frac{5π}{3}$.
当α=$\frac{π}{3}$,β=$\frac{4π}{3}$,不满足cosα+cosβ=1,舍去;
当α=$\frac{π}{3}$,β=$\frac{5π}{3}$,满足cosα+cosβ=1,此时α+β=2π.
当α=$\frac{5π}{3}$时,又0<α<β<2π,不满足sinα+sinβ=0,舍去.
综上可得:β+α=2π.
点评 本题考查了向量坐标运算及其相等、同角三角函数基本关系式、分类讨论方法,考查了推理能力与计算能力,属于中档题.

| A. | $\frac{3}{2}$ | B. | 3 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
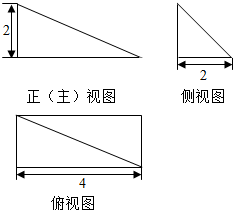
| A. | 12 | B. | 4 | C. | $\frac{16}{3}$ | D. | $\frac{8\sqrt{3}}{3}$ |
| A. | -$\sqrt{3}$ | B. | -$\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\sqrt{3}$ |
| A. | $\frac{\sqrt{15}}{3}$πm3 | B. | $\frac{32\sqrt{35}}{27}$πm3 | C. | $\frac{32\sqrt{35}}{81}$πm3 | D. | $\frac{128\sqrt{2}}{81}$πm3 |
| A. | 2 | B. | 2$\sqrt{3}$ | C. | 4 | D. | 6 |