题目内容
已知f(x)=ln(ax+b)-x,其中a>0,b>0,
(1)若f(x)为[0,+∞)上的减函数,求a,b应满足的关系;
(2)解不等式ln(1+
)-
≤ln2-1.
(1)若f(x)为[0,+∞)上的减函数,求a,b应满足的关系;
(2)解不等式ln(1+
x-
|
x-
|
考点:利用导数研究函数的单调性,对数的运算性质
专题:计算题,导数的综合应用
分析:(1)求出导数,由条件知f'(x)≤0对x≥0恒成立,对a,b分析即可;
(2)可令a=b=1,得到f(x)=ln(x+1)-x,运用单调性,将原不等式转化为f(
)≤f(1),即
≥1,解出即可.
(2)可令a=b=1,得到f(x)=ln(x+1)-x,运用单调性,将原不等式转化为f(
x-
|
x-
|
解答:
解:(1)f′(x)=
-1=
(a>0,b>0),
∵f(x)为[0,+∞)上的减函数
∴f'(x)≤0对x≥0恒成立,
∴a-b≤0即a≤b;
(2)在(1)中取a=b=1,即f(x)=ln(x+1)-x,
由(1)知f(x)在[0,+∞)上是减函数,
∴ln(1+
)-
≤ln2-1
即f(
)≤f(1),
∴
≥1,解得
≤x<0,或x≥
故所求不等式的解集为 [
,0)∪[
,+∞).
| a |
| ax+b |
| a-b-ax |
| ax+b |
∵f(x)为[0,+∞)上的减函数
∴f'(x)≤0对x≥0恒成立,
∴a-b≤0即a≤b;
(2)在(1)中取a=b=1,即f(x)=ln(x+1)-x,
由(1)知f(x)在[0,+∞)上是减函数,
∴ln(1+
x-
|
x-
|
即f(
x-
|
∴
x-
|
1-
| ||
| 2 |
1+
| ||
| 2 |
故所求不等式的解集为 [
1-
| ||
| 2 |
1+
| ||
| 2 |
点评:本题考查导数的综合运用,考查运用导数研究函数的单调性,以及应用函数的单调性解不等式,属于中档题.

练习册系列答案
相关题目
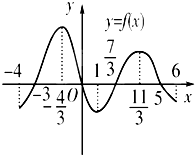 已知函数y=f(x)在定义域[-4,6]内可导,其图象如图,记y=f(x)的导函数为y=f′(x),则不等式f′(x)≤0的解集为( )
已知函数y=f(x)在定义域[-4,6]内可导,其图象如图,记y=f(x)的导函数为y=f′(x),则不等式f′(x)≤0的解集为( )A、[-
| ||||
B、[-3,0]∪[
| ||||
C、[-4,-
| ||||
| D、[-4,-3]∪[0,1]∪[5,6] |
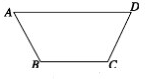 设计一个水渠,其横截面为等腰梯形(如图所示),要求满足条件AB+BC+CD=a(常数),∠ABC=120°,写出横截面的面积y与腰长x的关系式,并求它的定义域和值.
设计一个水渠,其横截面为等腰梯形(如图所示),要求满足条件AB+BC+CD=a(常数),∠ABC=120°,写出横截面的面积y与腰长x的关系式,并求它的定义域和值.