题目内容
已知某生产厂家的年利润y（单位：万元）与年产量x（单位：万件）的函数关系式为y=-
x3+49x-234则使该生产厂家获得最大年利润的年产量为（ ）
| 1 |
| 3 |
| A、13万件 | B、11万件 |
| C、9万件 | D、7万件 |
考点：利用导数研究函数的单调性
专题：导数的综合应用
分析：根据题意可知，要使该生产厂家获得最大年利润，只要求原函数在（0，+∞）上x取何值时取到最大值，所以先求y′，并令y′=0，判断函数的单调性及看有无极值点，从而求出使原函数取得最大值的x值．
解答：
解：y′=-x2+49，令-x2+49=0，∵x＞0，∴x=7．
∵x∈（0，7）时，y′＞0，x∈（7，+∞）时，y′＜0．
∴x=7时原函数取到极大值，并且也是最大值．
∴厂家获得最大年利润的年产量为7万件．
故选D．
∵x∈（0，7）时，y′＞0，x∈（7，+∞）时，y′＜0．
∴x=7时原函数取到极大值，并且也是最大值．
∴厂家获得最大年利润的年产量为7万件．
故选D．
点评：本题是个实际问题，所以能看出原函数的x取值范围为（0，+∞），而通过理解题意便会知道需要求的就是，找到x取何值时，原函数取到最大值．
练习册系列答案
轻松课堂单元测试AB卷系列答案
小题狂做系列答案
相关题目
如图正方体ABCD-A1B1C1D1，把一根拉紧的细绳两端分别系在AC1两点，此时这个正方体的正视图可能是（ ）
| A、①② | B、②③ | C、②④ | D、③④ |
过双曲线
-
=1（b＞a＞0）的右顶点A作斜率为1的直线，该直线与双曲线的一条渐近线y=
x交于点B，与另一条渐近线y=-
x交于点C，若A，B，C三点的横坐标成等比数列，则双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| b |
| a |
| b |
| a |
A、
| ||
B、
| ||
C、
| ||
D、
|
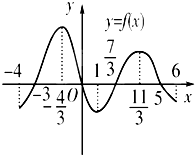已知函数y=f（x）在定义域[-4，6]内可导，其图象如图，记y=f（x）的导函数为y=f′（x），则不等式f′（x）≤0的解集为（ ）A、[-
| ||||
B、[-3，0]∪[
| ||||
C、[-4，-
| ||||
| D、[-4，-3]∪[0，1]∪[5，6] |
复数
=（ ）
| 3 |
| (1-i)2 |
| A、-i | ||
| B、i | ||
C、
| ||
D、-
|