题目内容
已知函数f(x)定义域为R,且对任意实数x,y满足f(x+y)=f(x)f(y),给出以下四个结论:
①若f(1)=2,则f(3)=8;
②若对任意x,恒有f(x)=c,其中c为常数,则c=0;
③若存在x0,使得f(x0)=0,则对任意x,恒有f(x)=0;
④若存在x0,使得f(x0)≠0,则对任意x,恒有f(x)>0;
其中正确的是 (只用填上正确选项的序号)
①若f(1)=2,则f(3)=8;
②若对任意x,恒有f(x)=c,其中c为常数,则c=0;
③若存在x0,使得f(x0)=0,则对任意x,恒有f(x)=0;
④若存在x0,使得f(x0)≠0,则对任意x,恒有f(x)>0;
其中正确的是
考点:抽象函数及其应用
专题:计算题,函数的性质及应用
分析:对于①,由条件可令x=y=1,再令x=1,y=2,即可得到f(3);对于②,对任意x,恒有f(x)=c,则f(x+y)=c,f(y)=c,由条件即可判断;对于③,由于存在x0,使得f(x0)=0,则有x∈R,f(x)=f(x-x0)f(x0)=0,即可判断;对于④,由于存在x0,使得f(x0)≠0,又f(x)=f2(
)≥0,即可判断.
| x |
| 2 |
解答:
解:对于①,由条件可令x=y=1,则f(2)=f2(1)=4,令x=1,y=2,
则f(3)=f(1)f(2)=2×4=8,故①对;
对于②,对任意x,恒有f(x)=c,则f(x+y)=c,f(y)=c,
则f(x+y)=f(x)f(y)有c=c2,即有c=0或c=1,故②错;
对于③,由于存在x0,使得f(x0)=0,则有x∈R,f(x)=f(x-x0)f(x0)=0,故③对;
对于④,由于存在x0,使得f(x0)≠0,又f(x)=f2(
)≥0,
则若存在
,使得f(
)=0,即有f(x0)=0,由③知,即f(x)=0,这与f(x)≥0矛盾,类比指数函数,
故④对.
故答案为:①③④
则f(3)=f(1)f(2)=2×4=8,故①对;
对于②,对任意x,恒有f(x)=c,则f(x+y)=c,f(y)=c,
则f(x+y)=f(x)f(y)有c=c2,即有c=0或c=1,故②错;
对于③,由于存在x0,使得f(x0)=0,则有x∈R,f(x)=f(x-x0)f(x0)=0,故③对;
对于④,由于存在x0,使得f(x0)≠0,又f(x)=f2(
| x |
| 2 |
则若存在
| x0 |
| 2 |
| x0 |
| 2 |
故④对.
故答案为:①③④
点评:本题考查抽象函数及运用,考查函数的自变量与函数值的关系,考查赋值法解决抽象函数值,考查推理能力,属于中档题和易错题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
函数y=
x4-x3的极值点的个数为( )
| 3 |
| 4 |
| A、0个 | B、1个 | C、2个 | D、3个 |
设集合S={x||x|<5},T={x|(x+7)(x-3)<0}.则S∩T=( )
| A、{x|-7<x<5 } |
| B、{x|3<x<5 } |
| C、{x|-5<x<3 } |
| D、{x|-7<x<-5 } |
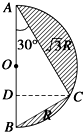 如图所示,半径为R的半圆内的阴影部分以直径AB所在直线为轴,旋转一周得到一几何体,∠BAC=30°,则此几何体的体积为
如图所示,半径为R的半圆内的阴影部分以直径AB所在直线为轴,旋转一周得到一几何体,∠BAC=30°,则此几何体的体积为