题目内容
已知函数f(x)=
(a>0).
(1)判断并证明函数f(x)的奇偶性;
(2)判断函数f(x)的单调性,并用函数的单调性定义给予证明.
| ax |
| x2-1 |
(1)判断并证明函数f(x)的奇偶性;
(2)判断函数f(x)的单调性,并用函数的单调性定义给予证明.
考点:函数奇偶性的判断,函数单调性的判断与证明
专题:函数的性质及应用
分析:(1)利用函数奇偶性的判断,首先求出定义域,然后判断f(x-)与f(x)的关系;
(2)利用函数的单调性定义判断函数的单调性.
(2)利用函数的单调性定义判断函数的单调性.
解答:
解:(1)函数的定义域为{x|x±1},定义域关于原点对称;
f(-x)=
=-
=-f(x),所以函数f(x)=
(a>0)为奇函数;
证明:函数的定义域为{x|x±1},定义域关于原点对称;
又有f(-x)=
=-
=-f(x),于是f(x)为奇函数;
(2)函数f(x)=
(a>0)在(-∞,-1);(-1,1);(1,+∞)三个区间上单调递减;
证明:设x1<x2<-1,则f(x2)-f(x1)=
-
=
=
又∵x1-x2<0,x1x2+1>0,(
-1)(
-1)>0且a>0,
∴f(x2)-f(x1)<0⇒f(x2)<f(x1),
∴f(x)在(-∞,-1)上为减函数;同理,f(x)在(-1,1)及(1,+∞)上均为减函数.
f(-x)=
| -ax |
| (-x)2-1 |
| ax |
| x2-1 |
| ax |
| x2-1 |
证明:函数的定义域为{x|x±1},定义域关于原点对称;
又有f(-x)=
| -ax |
| (-x)2-1 |
| ax |
| x2-1 |
(2)函数f(x)=
| ax |
| x2-1 |
证明:设x1<x2<-1,则f(x2)-f(x1)=
| ax2 | ||
|
| ax1 | ||
|
a[x2(
| ||||
(
|
| a(x1-x2)(x1x2+1) | ||||
(
|
又∵x1-x2<0,x1x2+1>0,(
| x | 2 2 |
| x | 2 1 |
∴f(x2)-f(x1)<0⇒f(x2)<f(x1),
∴f(x)在(-∞,-1)上为减函数;同理,f(x)在(-1,1)及(1,+∞)上均为减函数.
点评:本题考查了函数的奇偶性的判断和证明以及函数单调性的判断和证明,属于基础题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
化简
=( )
| 1-cos200° |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
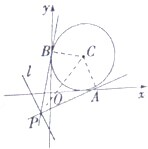 已知P是直线l:3x+4y+8=0上的动点,PA,PB是圆C:x2+y2-2x-2y+1=0的两条切线,A、B是切点.
已知P是直线l:3x+4y+8=0上的动点,PA,PB是圆C:x2+y2-2x-2y+1=0的两条切线,A、B是切点.