题目内容
6.若存在x0∈(0,1),使得(2-x0)e${\;}^{a{x}_{0}}$≥2+x0,则实数a的取值范围是( )| A. | (ln3,+∞) | B. | (1,+∞) | C. | ($\frac{1}{2}$,+∞) | D. | (0,+∞) |
分析 由存在x0∈(0,1),使ax≥ln(2+x)-ln(2-x)能成立,0<x<1.令f(x)=ln(2+x)-ln(2-x),则 ax≥f(x)能成立,故a大于或等于f′(x),再根据f′(x)的单调递增,且f′(0)=1,从而求得a的范围.
解答 解:∵存在x0∈(0,1),使得(2-x0)e${\;}^{a{x}_{0}}$≥2+x0,
∴${e}^{{ax}_{0}}$≥$\frac{2{+x}_{0}}{2{-x}_{0}}$>1,∴ax0≥ln(2+x0)-ln(2-x0),
即 ax≥ln(2+x)-ln(2-x)能成立,0<x<1.
令f(x)=ln(2+x)-ln(2-x),则 ax≥f(x)能成立(0<x<1),
故直线y=ax不能恒在函数y=f(x)的下方,
故直线y=ax的斜率a大于或等于f′(x).
则f′(x)=$\frac{1}{2+x}$+$\frac{1}{2-x}$=$\frac{4}{4{-x}^{2}}$>1,f(x)在(0,1)上单调递增.
∵x∈(0,1),∴f′(x)是增函数,又f′(0)=1,∴f′(x)>0,故 a>1,
故选:B.
点评 本题主要考查指数函数的单调性,利用导数研究函数的单调性,属于中档题.

练习册系列答案
相关题目
14.已知{an}是首项为1的等比数列,若Sn是{an}的前n项和,且28S3=S6,则数列{$\frac{1}{{a}_{n}}$}的前4项和为( )
| A. | $\frac{15}{8}$ | B. | 4 | C. | $\frac{40}{27}$ | D. | 40 |
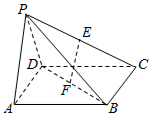 如图,四棱锥P-ABCD的底面是矩形,△PAD为等边三角形,且平面PAD⊥平面ABCD,E,F分别为PC和BD的中点.
如图,四棱锥P-ABCD的底面是矩形,△PAD为等边三角形,且平面PAD⊥平面ABCD,E,F分别为PC和BD的中点. 如图,圆柱O-O1中,AB为下底面圆O的直径,CD为上底面圆O1的直径,AB∥CD,点 E、F在圆O上,且AB∥EF,且AB=2,AD=1.
如图,圆柱O-O1中,AB为下底面圆O的直径,CD为上底面圆O1的直径,AB∥CD,点 E、F在圆O上,且AB∥EF,且AB=2,AD=1.