题目内容
11. 如图,圆柱O-O1中,AB为下底面圆O的直径,CD为上底面圆O1的直径,AB∥CD,点 E、F在圆O上,且AB∥EF,且AB=2,AD=1.
如图,圆柱O-O1中,AB为下底面圆O的直径,CD为上底面圆O1的直径,AB∥CD,点 E、F在圆O上,且AB∥EF,且AB=2,AD=1.(Ⅰ)求证:平面ADF⊥平面CBF;
(Ⅱ)若DF与底面所成角为$\frac{π}{4}$,求几何体EF-ABCD的体积.
分析 (Ⅰ)利用已知条件证明BF⊥平面ADF,然后证明平面ADF⊥平面CBF.
(Ⅱ)推出$∠AFD=\frac{π}{4}$,求出四棱锥F-ABCD的高为$\frac{{\sqrt{3}}}{2}$,底面面积SABCD=2,求出体积,然后之后求解几何体EF-ABCD的体积.
解答 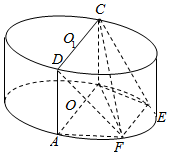 (Ⅰ)证明:由已知,AF⊥BF,AD⊥BF,且AF∩AD=A,故BF⊥平面ADF,
(Ⅰ)证明:由已知,AF⊥BF,AD⊥BF,且AF∩AD=A,故BF⊥平面ADF,
所以平面ADF⊥平面CBF.…(5分)
(Ⅱ)解:因AD垂直于底面,若DF与底面所成角为$\frac{π}{4}$,则$∠AFD=\frac{π}{4}$,故AF=1,
则四棱锥F-ABCD的高为$\frac{{\sqrt{3}}}{2}$,又SABCD=2,${V_{F-ABCD}}=\frac{1}{3}×\frac{{\sqrt{3}}}{2}×2=\frac{{\sqrt{3}}}{3}$;
三棱锥C-BEF的高为1,而△BEF中,BE=BF=1,∠BEF=120°,
所以${S_{BEF}}=\frac{{\sqrt{3}}}{4}$,则${V_{C-BEF}}=\frac{1}{3}×1×\frac{{\sqrt{3}}}{4}=\frac{{\sqrt{3}}}{12}$,
所以几何体EF-ABCD的体积为$\frac{{5\sqrt{3}}}{12}$.…(12分)
点评 本题考查直线与平面垂直,平面与平面垂直的判定定理的应用,几何体的体积的求法,考查转化思想以及空间想象能力计算能力.

练习册系列答案
相关题目
2.函数$f(x)=\sqrt{3}sinx+sin(\frac{π}{2}+x)$的一条对称轴是( )
| A. | $x=\frac{π}{6}$ | B. | $x=\frac{π}{3}$ | C. | $x=\frac{2π}{3}$ | D. | $x=\frac{5π}{6}$ |
6.若存在x0∈(0,1),使得(2-x0)e${\;}^{a{x}_{0}}$≥2+x0,则实数a的取值范围是( )
| A. | (ln3,+∞) | B. | (1,+∞) | C. | ($\frac{1}{2}$,+∞) | D. | (0,+∞) |
3.已知全集U={0,1,2,3,4,5,6},集合A={0,1,3},集合B={2,6},则(∁UA)∩(∁UB)为( )
| A. | {5,6} | B. | {4,5} | C. | {0,3} | D. | {2,6} |
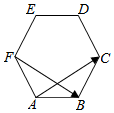
20.如图,在正六边形ABCDEF中,|$\overrightarrow{AC}$+$\overrightarrow{AE}$|=6,则$\overrightarrow{AF}$•$\overrightarrow{FB}$等于( )

| A. | -6 | B. | 6 | C. | -2$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
1.已知|$\overrightarrow{a}$|=4,|$\overrightarrow{b}$|=3,$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为60°,则满足条件|m$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{33}$的所有实数m之和为( )
| A. | -$\frac{3}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{4}$ | D. | -$\frac{1}{4}$ |