题目内容
6.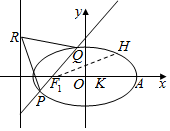 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),正三角形PQR的顶点R在C的左准线l上,P、Q在椭圆上,且线段PQ经过左焦点F1,KPQ=1.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),正三角形PQR的顶点R在C的左准线l上,P、Q在椭圆上,且线段PQ经过左焦点F1,KPQ=1.(1)求椭圆C的离心率;
(2)椭圆上是否存在关于直线PQ对称的两点,请说明理由;
(3)设H为椭圆上一动点,K是x正半轴上一定点,满足OA=3OK(A为椭圆右顶点),当HK+HF1的最大值为5+$\sqrt{6}$时,求椭圆的方程.
分析 (1)设左焦点F1(-c,0),右焦点F2(c,0),直线PQ的方程为y=x+c,代入椭圆方程,运用韦达定理和弦长公式,再由中点坐标公式,可得PQ的垂直平分线方程,求得R的坐标,由点到直线的距离公式可得R到PQ的距离,由等边三角形的性质,可得方程,即可得到a,c的关系,即可得到离心率;
(2)由(1)中的垂直平分线方程,代入椭圆方程,运用韦达定理和中点坐标公式,代入PQ的方程,检验是否为中点,即可判断存在性;
(3)运用椭圆的定义可得HK+HF1=HK+2a-HF2=2a-(HF2-HK)≤2a+KF2,当H,K,F2在x轴上,且H为右顶点时,取得最大值,再由离心率,计算即可得到a,b,进而得到椭圆方程.
解答 解:(1)设左焦点F1(-c,0),右焦点F2(c,0),
直线PQ的方程为y=x+c,
代入椭圆方程b2x2+a2y2=a2b2,可得
(b2+a2)x2+2ca2x+a2c2-a2b2=0,
设P(x1,y1),Q(x2,y2),
可得x1+x2=-$\frac{2c{a}^{2}}{{a}^{2}+{b}^{2}}$,x1x2=$\frac{{a}^{2}{c}^{2}-{a}^{2}{b}^{2}}{{a}^{2}+{b}^{2}}$,
|PQ|=$\sqrt{2}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{2}$•$\sqrt{\frac{4{c}^{2}{a}^{4}}{({a}^{2}+{b}^{2})^{2}}-\frac{4{a}^{2}({c}^{2}-{b}^{2})}{{a}^{2}+{b}^{2}}}$=$\frac{4a{b}^{2}}{{a}^{2}+{b}^{2}}$,
PQ的中点为(-$\frac{c{a}^{2}}{{a}^{2}+{b}^{2}}$,$\frac{c{b}^{2}}{{a}^{2}+{b}^{2}}$),
可得PQ的垂直平分线方程为y-$\frac{c{b}^{2}}{{a}^{2}+{b}^{2}}$=-(x+$\frac{c{a}^{2}}{{a}^{2}+{b}^{2}}$),
即为y=-x-$\frac{{c}^{3}}{{a}^{2}+{b}^{2}}$,
令x=-$\frac{{a}^{2}}{c}$,则y=$\frac{{a}^{2}}{c}$-$\frac{{c}^{3}}{{a}^{2}+{b}^{2}}$=$\frac{{b}^{2}({c}^{2}+2{a}^{2})}{c({a}^{2}+{b}^{2})}$,
即为R(-$\frac{{a}^{2}}{c}$,$\frac{{b}^{2}({c}^{2}+2{a}^{2})}{c({a}^{2}+{b}^{2})}$),
R到直线PQ的距离为d=$\frac{|-\frac{{a}^{2}}{c}+c-\frac{{b}^{2}({c}^{2}+2{a}^{2})}{c({a}^{2}+{b}^{2})}|}{\sqrt{2}}$=$\frac{4{a}^{2}{b}^{2}}{\sqrt{2}c({a}^{2}+{b}^{2})}$,
由△PQR为等边三角形,可得d=$\frac{\sqrt{3}}{2}$|PQ|,
即有$\frac{4{a}^{2}{b}^{2}}{\sqrt{2}c({a}^{2}+{b}^{2})}$=$\frac{\sqrt{3}}{2}$•$\frac{4a{b}^{2}}{{a}^{2}+{b}^{2}}$,
化简可得$\sqrt{6}$c=2a,可得e=$\frac{c}{a}$=$\frac{\sqrt{6}}{3}$;
(2)设a=3t,由离心率可得c=$\sqrt{6}$t,b=$\sqrt{3}$t,t>0,
由(1)可得,PQ的垂直平分线方程为y=-x-$\frac{{c}^{3}}{{a}^{2}+{b}^{2}}$,
即为y=-x-$\frac{\sqrt{6}}{2}$t,
代入椭圆方程x2+3y2=9t2,可得4x2+3$\sqrt{6}$tx-$\frac{9{t}^{2}}{2}$=0,
即有x1+x2=-$\frac{3\sqrt{6}t}{4}$,弦的中点为(-$\frac{3\sqrt{6}t}{4}$,$\frac{\sqrt{6}}{4}$t),
代入直线PQ,可得$\frac{\sqrt{6}}{4}$t=-$\frac{3\sqrt{6}t}{4}$+$\sqrt{6}$t,方程成立.
故椭圆上存在关于直线PQ对称的两点;
(3)由OA=3OK,可得K($\frac{1}{3}$a,0),F2(c,0),
由椭圆的定义可得,HK+HF1=HK+2a-HF2=2a-(HF2-HK)
≤2a+KF2=2a+c-$\frac{1}{3}$a=c+$\frac{5a}{3}$,
当H,K,F2在x轴上,且H为右顶点时,取得最大值c+$\frac{5a}{3}$,
即有c+$\frac{5a}{3}$=5+$\sqrt{6}$,又$\sqrt{6}$c=2a,
解得c=$\sqrt{6}$,a=3,b=$\sqrt{3}$,
即有椭圆的方程为$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{3}$=1.
点评 本题考查椭圆的方程和离心率的求法,注意运用直线和椭圆方程联立,运用韦达定理和弦长公式,同时考查点关于直线的对称的求法,以及三点共线时取最值的方法,考查化简整理的运算能力,综合性强,属于难题.

 备战中考寒假系列答案
备战中考寒假系列答案| 日期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 |
| 价格x(元) | 9 | 9.5 | 10 | 10.5 | 11 |
| 销售量y(万件) | 11 | 10 | 8 | 6 | 5 |
| A. | 7.66万件 | B. | 7.86万件 | C. | 8.06万件 | D. | 7.36万件 |
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | b=2,c=-3 | B. | b=2,c=5 | C. | b=-2,c=-3 | D. | b=-2,c=5 |
| A. | 1 | B. | $\frac{1}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
| A. | ($\frac{\sqrt{6}}{3}$,1) | B. | (0,$\frac{\sqrt{6}}{3}$) | C. | (0,$\frac{2}{3}$) | D. | ($\frac{2}{3}$,1) |
| A. | {3,4,5} | B. | {4,5} | C. | {-1,1} | D. | {-1,1,2} |