题目内容
15.设点A1、A2分别为椭圆C:$\frac{y^2}{a^2}+\frac{x^2}{b^2}$=1(a>b>0)的下顶点和上顶点,若在椭圆上存在点P使得${k}_{P{A}_{1}}$•${k}_{P{A}_{2}}$>-3,则椭圆C的离心率的取值范围是( )| A. | ($\frac{\sqrt{6}}{3}$,1) | B. | (0,$\frac{\sqrt{6}}{3}$) | C. | (0,$\frac{2}{3}$) | D. | ($\frac{2}{3}$,1) |
分析 根据题意设P(bsinα,acosα),求出${k}_{P{A}_{1}}$,${k}_{P{A}_{2}}$,结合${k}_{P{A}_{1}}$•${k}_{P{A}_{2}}$>-3及隐含条件列式求得椭圆离心率的取值范围.
解答 解:设P(bsinα,acosα),A1(0,-a),A2(0,a).
∴${k}_{P{A}_{1}}=\frac{acosα+a}{bsinα},{k}_{P{A}_{2}}=\frac{acosα-a}{bsinα}$,
由${k}_{P{A}_{1}}$•${k}_{P{A}_{2}}$>-3,得$\frac{{a}^{2}(co{s}^{2}α-1)}{{b}^{2}si{n}^{2}α}$>-3,
即$-\frac{{a}^{2}si{n}^{2}α}{{b}^{2}si{n}^{2}α}>-3$,∴$\frac{{a}^{2}}{{b}^{2}}<3$,
则a2<3(a2-c2),∴2a2>3c2,
得$\frac{{c}^{2}}{{a}^{2}}<\frac{2}{3}$,即e∈(0,$\frac{\sqrt{6}}{3}$),
故选:B.
点评 本题考查椭圆的简单性质,考查由两点坐标求斜率公式,正确设出p的坐标是求解本题的关键,是中档题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
5.i为虚数单位,负数i2016的共轭复数为( )
| A. | 1 | B. | i | C. | -1 | D. | -i |
7.已知两点P(4,0),Q(0,2),则以线段PQ为直径的圆的方程是( )
| A. | (x+2)2+(y+1)2=5 | B. | (x-2)2+(y-1)2=10 | C. | (x-2)2+(y-1)2=5 | D. | (x+2)2+(y+1)2=10 |
4.已知y=2cosx(x∈R),则( )
| A. | -1≤y≤1 | B. | y≤2 | C. | -2≤y≤2 | D. | y≥-2 |
17.已知集合M={(x,y)|x=0},N={(x,y)|y=x+2},则M∩N=( )
| A. | {0} | B. | {(0,2)} | C. | {2} | D. | {(2,0)} |
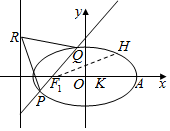 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),正三角形PQR的顶点R在C的左准线l上,P、Q在椭圆上,且线段PQ经过左焦点F1,KPQ=1.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),正三角形PQR的顶点R在C的左准线l上,P、Q在椭圆上,且线段PQ经过左焦点F1,KPQ=1.