题目内容
1．若1+2i（i为虚数单位）是实系数方程x2+bx+c=0的一个复数根，则（ ）| A． | b=2，c=-3 | B． | b=2，c=5 | C． | b=-2，c=-3 | D． | b=-2，c=5 |
分析 利用实系数一元二次的虚根成对原理、根与系数的关系即可得出．
解答 解：∵1+2i是关于x的实系数方程x2+bx+c=0的一个复数根，
∴1-2i是关于x的实系数方程x2+bx+c=0的一个复数根，
∴$\left\{\begin{array}{l}{1+2i+1-2i=-b}\\{（1+2i）（1-2i）=c}\end{array}\right.$，解得b=-2，c=5．
故选：D．
点评 本题考查复数相等的充要条件，解题的关键是熟练掌握复数相等的充要条件，能根据它得到关于实数的方程，本题考查了转化的思想，属于基本计算题
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
期末集结号系列答案
相关题目
11．已知向量$\overrightarrow a，\overrightarrow b$的夹角为60°，且|$\overrightarrow{a}$|=1，|$\overrightarrow{a}$-2$\overrightarrow{b}$|=$\sqrt{21}$，则|$\overrightarrow{b}$|=（ ）
| A． | $\sqrt{2}$ | B． | $\frac{3}{2}$ | C． | $\frac{5}{2}$ | D． | $2\sqrt{2}$ |
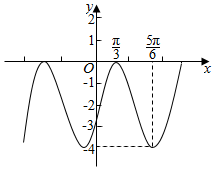已知函数f（x）=sinωx（sinωx+2$\sqrt{3}$cosωx）+sin（ωx-$\frac{π}{4}$）sin（ωx+$\frac{π}{4}$）（其中ω为常数，且ω＞0），函数g（x）=f（x）-$\frac{5}{2}$的部分图象如图所示．
9．已知Z=$\frac{2i}{1+i}$（i为虚数单位），则Z的共轭复数在复平面内对应的点位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
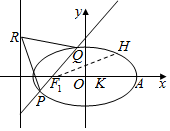如图，已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），正三角形PQR的顶点R在C的左准线l上，P、Q在椭圆上，且线段PQ经过左焦点F1，KPQ=1．