题目内容
14.已知函数$f(x)=|{x-a}|+|{x-\frac{1}{2}}|,x∈R$(Ⅰ)当$a=\frac{5}{2}$时,解不等式f(x)≤x+10;
(Ⅱ)关于x的不等式f(x)≥a在R上恒成立,求实数a的取值范围.
分析 (Ⅰ)通过讨论x的范围,求出不等式的解集,取并集即可;(Ⅱ)根据绝对值的意义求出f(x)的最小值,从而求出a的范围.
解答 解:(Ⅰ)当$a=\frac{5}{2}$时,
$f(x)=|{x-a}|+|{x-\frac{1}{2}}|=\left\{{\begin{array}{l}{-2x+3,}&{x<\frac{1}{2}}\\{2,}&{\frac{1}{2}≤x≤\frac{5}{2}}\\{2x-3,}&{x>\frac{5}{2}}\end{array}}\right.$,
①当$x<\frac{1}{2}$时,由f(x)≤x+10得-2x+3≤x+10,
解得$x≥-\frac{7}{3}$,此时$-\frac{7}{3}≤x<\frac{1}{2}$;
②当$\frac{1}{2}≤x≤\frac{5}{2}$时,由f(x)≤x+10得2≤x+10,
解得x≥-8,此时$\frac{1}{2}≤x≤\frac{5}{2}$;..
③当$x>\frac{5}{2}$时,由f(x)≤x+10得2≤x+10,
解得x≤13,此时$\frac{5}{2}<x≤13$;
综上,不等式f(x)≤x+10的解集为$\left\{{x\left|{-\frac{7}{3}≤x≤13}\right.}\right\}$;
(Ⅱ)由绝对值不等式的性质得:
$f(x)=|{x-a}|+|{x-\frac{1}{2}}|≥|{({x-a})-({x-\frac{1}{2}})}|=|{-a+\frac{1}{2}}|$,
∴f(x)的最小值为$|{-a+\frac{1}{2}}|$,
由题意得$|{-a+\frac{1}{2}}|≥a$,解得$a≤\frac{1}{4}$,
∴实数a的取值范围为$({-∞,\frac{1}{4}}]$.
点评 本题考查了解绝对值不等式问题,绝对值的几何意义,考查分类讨论思想,是一道中档题.

| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分又不必要条件 |
| A. | 1 | B. | i | C. | -1 | D. | -i |
点数分别为x,y,记事件A为“x,y都为偶数且x≠y”,则A发生的概率P(A)为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{12}$ |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | -1≤y≤1 | B. | y≤2 | C. | -2≤y≤2 | D. | y≥-2 |
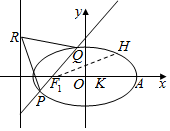 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),正三角形PQR的顶点R在C的左准线l上,P、Q在椭圆上,且线段PQ经过左焦点F1,KPQ=1.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),正三角形PQR的顶点R在C的左准线l上,P、Q在椭圆上,且线段PQ经过左焦点F1,KPQ=1.