题目内容
17.已知命题p:双曲线C为等轴双曲线,命题q:双曲线C的离心率为$\sqrt{2}$,则命题p是命题q成立的( )| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 双曲线C的离心率为$\sqrt{2}$,求出双曲线方程判断是不是等轴双曲线,以及双曲线C为等轴双曲线求出离心率,即可判断充要条件.
解答 解:双曲线C的离心率为$\sqrt{2}$,所以c=$\sqrt{2}$a,并且a=b,所以双曲线为等轴双曲线,
对于命题p,双曲线C为等轴双曲线,所以a=b,c=$\sqrt{2}$a,所以e=$\sqrt{2}$.
所以命题“q:双曲线C的离心率为$\sqrt{2}$”,命题“q:双曲线C为等轴双曲线”.
则p是q的充要条件.
故选:C.
点评 本题考查双曲线的离心率与等轴双曲线的关系,充要条件的应用.

练习册系列答案
相关题目
5.i为虚数单位,负数i2016的共轭复数为( )
| A. | 1 | B. | i | C. | -1 | D. | -i |
2.先后掷两次骰子(骰子的六个面上分别有1,2,3,4,5,6个点),落在水平桌面后,记正面朝上的
点数分别为x,y,记事件A为“x,y都为偶数且x≠y”,则A发生的概率P(A)为( )
点数分别为x,y,记事件A为“x,y都为偶数且x≠y”,则A发生的概率P(A)为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{12}$ |
9.已知Z=$\frac{2i}{1+i}$(i为虚数单位),则Z的共轭复数在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
7.已知两点P(4,0),Q(0,2),则以线段PQ为直径的圆的方程是( )
| A. | (x+2)2+(y+1)2=5 | B. | (x-2)2+(y-1)2=10 | C. | (x-2)2+(y-1)2=5 | D. | (x+2)2+(y+1)2=10 |
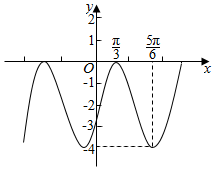 已知函数f(x)=sinωx(sinωx+2$\sqrt{3}$cosωx)+sin(ωx-$\frac{π}{4}$)sin(ωx+$\frac{π}{4}$)(其中ω为常数,且ω>0),函数g(x)=f(x)-$\frac{5}{2}$的部分图象如图所示.
已知函数f(x)=sinωx(sinωx+2$\sqrt{3}$cosωx)+sin(ωx-$\frac{π}{4}$)sin(ωx+$\frac{π}{4}$)(其中ω为常数,且ω>0),函数g(x)=f(x)-$\frac{5}{2}$的部分图象如图所示.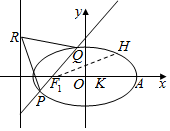 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),正三角形PQR的顶点R在C的左准线l上,P、Q在椭圆上,且线段PQ经过左焦点F1,KPQ=1.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),正三角形PQR的顶点R在C的左准线l上,P、Q在椭圆上,且线段PQ经过左焦点F1,KPQ=1.