题目内容
18.在△ABC中,M是AB的中点,N是AC上一点,且$\overrightarrow{NC}$=2$\overrightarrow{AN}$,BN与CM相交于一点P.$\overrightarrow{AP}$=$λ\overrightarrow{AB}$+$μ\overrightarrow{AC}$,则λ+μ=( )| A. | 1 | B. | $\frac{1}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
分析 过N作AB的平行线,交CM于点D,利用平行线的性质得到线段的比例关系,结合向量的线性表示得到解答.
解答 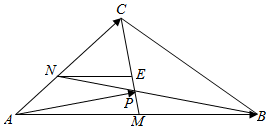 解:由已知,在△ABC中,$\overrightarrow{AM}$=$\overrightarrow{MB}$,且$\overrightarrow{NC}$=2$\overrightarrow{AN}$,已知BN与CM交于点P,过N作AB的平行线,交CM于点E,
解:由已知,在△ABC中,$\overrightarrow{AM}$=$\overrightarrow{MB}$,且$\overrightarrow{NC}$=2$\overrightarrow{AN}$,已知BN与CM交于点P,过N作AB的平行线,交CM于点E,
在三角形ACM中,CN:CA=NE:AM=2:3,
所以NE:MB=NP:PB=EP:PM=2:3,
所以$\overrightarrow{NP}$=$\frac{2}{5}$$\overrightarrow{NB}$,
故$\overrightarrow{AP}$=$\overrightarrow{AN}$+$\overrightarrow{NP}$=$\frac{1}{3}$$\overrightarrow{AC}$+$\frac{2}{5}$$\overrightarrow{NB}$
=$\frac{1}{3}$$\overrightarrow{AC}$+$\frac{2}{5}$($\overrightarrow{NA}$+$\overrightarrow{AB}$)=$\frac{2}{5}$$\overrightarrow{AB}$+$\frac{1}{5}$$\overrightarrow{AC}$,
故λ+μ=$\frac{2}{5}$+$\frac{1}{5}$=$\frac{3}{5}$,
故选:C.
点评 本题考查了向量的三角形法则和平面向量基本定理,属于基础题.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
9.已知Z=$\frac{2i}{1+i}$(i为虚数单位),则Z的共轭复数在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
7.已知两点P(4,0),Q(0,2),则以线段PQ为直径的圆的方程是( )
| A. | (x+2)2+(y+1)2=5 | B. | (x-2)2+(y-1)2=10 | C. | (x-2)2+(y-1)2=5 | D. | (x+2)2+(y+1)2=10 |
20.圆(x-1)2+y2=1被直线$x-\sqrt{3}y=0$分成两段圆弧,则较短弧长与较长弧长之比为( )
| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 1:5 |
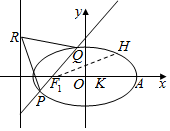 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),正三角形PQR的顶点R在C的左准线l上,P、Q在椭圆上,且线段PQ经过左焦点F1,KPQ=1.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),正三角形PQR的顶点R在C的左准线l上,P、Q在椭圆上,且线段PQ经过左焦点F1,KPQ=1.