Question

若数列满足，则称数列为“平方递推数列”．已知数列中，，点在函数的图象上，其中为正整数．

（1）证明数列是“平方递推数列”，且数列为等比数列；

（2）设（1）中“平方递推数列”的前项积为，即，求；

（3）在（2）的条件下，记，求数列的前项和，并求使 的的最小值．

Answer 1

解证（1）由题意得：，即 ，则是“平方递推数列”． 

对两边取对数得 ，

所以数列是以为首项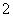，为公比的等比数列

（2）由（1）知   

          

(3）              

又，即   

又，所以．