题目内容
下面说法中,正确的是( )
①一个平面内只有一对不共线向量可作为表示该平面内所有向量的基底;
②一个平面内由无数多对不共线向量可作为表示该平面内所有向量的基底;
③零向量不可作为基底中的向量;
④对于平面内的任一向量
和一组基底
,
,使
=λ
+μ
成立的实数对一定是唯一的.
①一个平面内只有一对不共线向量可作为表示该平面内所有向量的基底;
②一个平面内由无数多对不共线向量可作为表示该平面内所有向量的基底;
③零向量不可作为基底中的向量;
④对于平面内的任一向量
| a |
| e1 |
| e2 |
| a |
| e1 |
| e2 |
| A、②④ | B、②③④ |
| C、①③ | D、①③④ |
考点:命题的真假判断与应用
专题:综合题,推理和证明
分析:本题考查平面向量基本定理,由定理知可作为平面内所有向量的一组基底的两个向量必是不共线的,由此关系对四个选项作出判断,得出正确选项.
解答:
解:根据平面向量基本定理知:
①一个平面内任何一对不平行的向量可作为表示该平面所有向量的基,故错;
②一个平面内有无数多对不平行向量都可作为表示该平面内所有向量的基;故正确;
③零向量不可作为基底中的向量,正确;
④对于平面内的任一向量
和一组基底
,
,使
=λ
+μ
成立的实数对一定是唯一的,根据平面向量基本定理可知正确.
故选:B
①一个平面内任何一对不平行的向量可作为表示该平面所有向量的基,故错;
②一个平面内有无数多对不平行向量都可作为表示该平面内所有向量的基;故正确;
③零向量不可作为基底中的向量,正确;
④对于平面内的任一向量
| a |
| e1 |
| e2 |
| a |
| e1 |
| e2 |
故选:B
点评:本题考查平面向量基本定理,解题的关键是理解定理,明确概念,可作为基底的两个向量必不共线.

练习册系列答案
相关题目
已知随机变量ξ服从正态分布N(1,σ2),若p(ξ>2)=0.16,则p{0<ξ<1}=( )
| A、0.68 | B、0.32 |
| C、0.42 | D、0.34 |
若执行如图的程序框图,输出S的值为4,则判断框中应填入的条件是( )
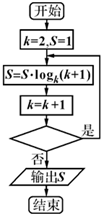

| A、k<14? |
| B、k<15? |
| C、k<16? |
| D、k<17? |
设两个向量
=(n+2,n-cos2x),
=(m,
+sinx),其中m,n为实数,若存在实数x使得
=2
,则m的取值范围为( )
| a |
| b |
| m |
| 2 |
| a |
| b |
| A、[1,4] |
| B、[0,4] |
| C、[0,2] |
| D、[-6,-2] |
