题目内容
计算:
.
| cos(3π-α)tan(5π+α) |
| sin(3π+α) |
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:利用三角函数的诱导公式化简求值.
解答:
解:原式=
=
=1.
| -cosαtanα |
| -sinα |
cosα
| ||
| sinα |
点评:本题考查了利用三角函数的诱导公式化简三角函数式;关键是熟记诱导公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下面说法中,正确的是( )
①一个平面内只有一对不共线向量可作为表示该平面内所有向量的基底;
②一个平面内由无数多对不共线向量可作为表示该平面内所有向量的基底;
③零向量不可作为基底中的向量;
④对于平面内的任一向量
和一组基底
,
,使
=λ
+μ
成立的实数对一定是唯一的.
①一个平面内只有一对不共线向量可作为表示该平面内所有向量的基底;
②一个平面内由无数多对不共线向量可作为表示该平面内所有向量的基底;
③零向量不可作为基底中的向量;
④对于平面内的任一向量
| a |
| e1 |
| e2 |
| a |
| e1 |
| e2 |
| A、②④ | B、②③④ |
| C、①③ | D、①③④ |
从数字1,2,3中任取两个不同的数字构成一个两位数,则这个两位数大于30的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=log3(10x+
-2),则f(x)的值域为( )
| 1 |
| 10x |
| A、(-∞,-3) |
| B、(-3,3) |
| C、[0,+∞) |
| D、(-∞,+∞) |
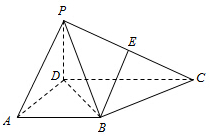 如图,在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,E为PC的中点,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=1,CD=2
如图,在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,E为PC的中点,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=1,CD=2