题目内容
为了进一步激发同学们的学习热情,某班级建立了理科.文科两个学习兴趣小组,两组的人数如下表所示.现采用分层抽样的方法(层内采用简单随机抽样)从两组中共抽取3名同学进行测试.
(1)求从理科组抽取的同学中至少有1名女同学的概率;
(2)记ξ为抽取的3名同学中男同学的人数,求随机变量ξ的分布列和数学期望.
| 组别 性别 | 理科 | 文科 |
| 男 | 5 | 1 |
| 女 | 3 | 3 |
(2)记ξ为抽取的3名同学中男同学的人数,求随机变量ξ的分布列和数学期望.
考点:离散型随机变量的期望与方差,古典概型及其概率计算公式,离散型随机变量及其分布列
专题:概率与统计
分析:(1)两小组的总人数之比为8:4=2:1,共抽取3人,所以理科组抽取2人,文科组抽取1人,从理科组抽取的同学中至少有1名女同学的情况有:一男一女、两女,由此能求出从理科组抽取的同学中至少有1名女同学的概率.
(2)由题意可知ξ的所有可能取值为0,1,2,3,分别求出相应的概率,由此能求出随机变量ξ的分布列和数学期望.
(2)由题意可知ξ的所有可能取值为0,1,2,3,分别求出相应的概率,由此能求出随机变量ξ的分布列和数学期望.
解答:
解:(1)两小组的总人数之比为8:4=2:1,
共抽取3人,所以理科组抽取2人,
文科组抽取1人,…(2分)
从理科组抽取的同学中至少有1名女同学的情况有:一男一女、两女,
所以所求的概率为:P=
=
.…(4分)
(2)由题意可知ξ的所有可能取值为0,1,2,3,…(5分)
相应的概率分别是:
P(ξ=0)=
=
,
P(ξ=1)=
+
=
,
P(ξ=2)=
+
=
,
P(ξ=3)=
=
,…(9分)
所以ξ的分布列为:
Eξ=1×
+2×
+3×
=
.
共抽取3人,所以理科组抽取2人,
文科组抽取1人,…(2分)
从理科组抽取的同学中至少有1名女同学的情况有:一男一女、两女,
所以所求的概率为:P=
| ||||||
|
| 9 |
| 14 |
(2)由题意可知ξ的所有可能取值为0,1,2,3,…(5分)
相应的概率分别是:
P(ξ=0)=
| ||||
|
| ||
|
| 9 |
| 112 |
P(ξ=1)=
| ||||
|
| ||
|
| ||
|
| 1 | ||
|
| 48 |
| 112 |
P(ξ=2)=
| ||||
|
| 1 | ||
|
| ||
|
| ||
|
| 45 |
| 112 |
P(ξ=3)=
| ||
|
| 1 | ||
|
| 10 |
| 112 |
所以ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 48 |
| 112 |
| 45 |
| 112 |
| 10 |
| 112 |
| 3 |
| 2 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,解题时要认真审题,注意排列组合知识的合理运用.

练习册系列答案
相关题目
设双曲线
+
=1的离心率为2,且一个焦点与抛物线x2=8y的焦点相同,则此双曲线的方程为( )
| x2 |
| m |
| y2 |
| n |
A、
| ||||
B、
| ||||
C、y2-
| ||||
D、
|
(x2+
-2)3展开式中的常数项为( )
| 1 |
| x2 |
| A、-8 | B、-12 |
| C、-20 | D、20 |
下面说法中,正确的是( )
①一个平面内只有一对不共线向量可作为表示该平面内所有向量的基底;
②一个平面内由无数多对不共线向量可作为表示该平面内所有向量的基底;
③零向量不可作为基底中的向量;
④对于平面内的任一向量
和一组基底
,
,使
=λ
+μ
成立的实数对一定是唯一的.
①一个平面内只有一对不共线向量可作为表示该平面内所有向量的基底;
②一个平面内由无数多对不共线向量可作为表示该平面内所有向量的基底;
③零向量不可作为基底中的向量;
④对于平面内的任一向量
| a |
| e1 |
| e2 |
| a |
| e1 |
| e2 |
| A、②④ | B、②③④ |
| C、①③ | D、①③④ |
从数字1,2,3中任取两个不同的数字构成一个两位数,则这个两位数大于30的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
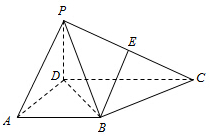 如图,在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,E为PC的中点,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=1,CD=2
如图,在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,E为PC的中点,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=1,CD=2