题目内容
求下列函数的最大值和最小值,并写出取得最大值和最小值时的自变量x的值.
(1)y=3cosx,x∈(-
,
];
(2)y=-
sinx,x∈(-
,
).
(1)y=3cosx,x∈(-
| π |
| 6 |
| 4π |
| 3 |
(2)y=-
| 1 |
| 2 |
| 5π |
| 6 |
| 3π |
| 4 |
考点:三角函数的最值
专题:三角函数的求值
分析:(1)由条件结合余弦函数的图象特征求出写出函数取得最大值和最小值时的自变量x的值.
(2)由条件结合正弦函数的图象特征求出写出函数取得最大值和最小值时的自变量x的值.
(2)由条件结合正弦函数的图象特征求出写出函数取得最大值和最小值时的自变量x的值.
解答:
解:(1)根据y=3cosx,x∈(-
,
],可得当x=0时,函数y取得最大值为3;当x=π时,函数y取得最小值为-3.
(2)根据y=-
sinx,x∈(-
,
),可得当x=-
时,函数y取得最大值为
;当x=
时,函数y取得最小值为-
.
| π |
| 6 |
| 4π |
| 3 |
(2)根据y=-
| 1 |
| 2 |
| 5π |
| 6 |
| 3π |
| 4 |
| π |
| 2 |
| 1 |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
点评:本题主要考查正弦函数、余弦函数的最值,属于基础题.

练习册系列答案
相关题目
已知A、B、C三点不共线,对平面ABC外的任一点O,下列条件中能确定定点M与点A、B、C一定共面的是( )
A、
| ||||||||||||||
B、
| ||||||||||||||
C、
| ||||||||||||||
D、
|
设双曲线
+
=1的离心率为2,且一个焦点与抛物线x2=8y的焦点相同,则此双曲线的方程为( )
| x2 |
| m |
| y2 |
| n |
A、
| ||||
B、
| ||||
C、y2-
| ||||
D、
|
如果两个函数的图象经过平移后能够重合,那么这两个函数称为“伴侣”函数,下列函数中与g(x)=sinx+cosx能构成“伴侣”函数的是( )
A、f(x)=
| ||||||
| B、f(x)=1+sinx | ||||||
C、f(x)=sin
| ||||||
D、f(x)=2cos
|
(x2+
-2)3展开式中的常数项为( )
| 1 |
| x2 |
| A、-8 | B、-12 |
| C、-20 | D、20 |
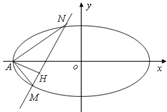 已知椭圆C:
已知椭圆C: