题目内容
已知随机变量ξ服从正态分布N(1,σ2),若p(ξ>2)=0.16,则p{0<ξ<1}=( )
| A、0.68 | B、0.32 |
| C、0.42 | D、0.34 |
考点:正态分布曲线的特点及曲线所表示的意义
专题:计算题,概率与统计
分析:根据随机变量ξ服从正态分布,知正态曲线的对称轴是x=1,依据正态分布对称性,即可求得答案.
解答:
解:随机变量ξ服从正态分布N(1,σ2),
∴曲线关于x=1对称,
∴P(0<ξ<1)=P(1<ξ<2)=0.5-P(ξ>2)=0.34.
故选:D.
∴曲线关于x=1对称,
∴P(0<ξ<1)=P(1<ξ<2)=0.5-P(ξ>2)=0.34.
故选:D.
点评:本题考查正态分布曲线的特点及曲线所表示的意义,本题解题的关键是利用正态曲线的对称性,是一个基础题.

练习册系列答案
相关题目
(x2+
-2)3展开式中的常数项为( )
| 1 |
| x2 |
| A、-8 | B、-12 |
| C、-20 | D、20 |
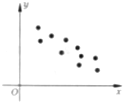 设(x1,y1),(x2,y2),…(xn,yn)是变量x,和y的n个样本点,直线l是由这样样本点通过最小二乘法得到的线性回归方程(如图),则下列结论中正确的是( )
设(x1,y1),(x2,y2),…(xn,yn)是变量x,和y的n个样本点,直线l是由这样样本点通过最小二乘法得到的线性回归方程(如图),则下列结论中正确的是( )| A、x和y正相关 |
| B、x和y的相关系数为直线l的斜率 |
| C、当n为偶数时,分布在l两侧的样本点的个数一定相同 |
| D、x和y的相关系数在-1到0之间 |
下面说法中,正确的是( )
①一个平面内只有一对不共线向量可作为表示该平面内所有向量的基底;
②一个平面内由无数多对不共线向量可作为表示该平面内所有向量的基底;
③零向量不可作为基底中的向量;
④对于平面内的任一向量
和一组基底
,
,使
=λ
+μ
成立的实数对一定是唯一的.
①一个平面内只有一对不共线向量可作为表示该平面内所有向量的基底;
②一个平面内由无数多对不共线向量可作为表示该平面内所有向量的基底;
③零向量不可作为基底中的向量;
④对于平面内的任一向量
| a |
| e1 |
| e2 |
| a |
| e1 |
| e2 |
| A、②④ | B、②③④ |
| C、①③ | D、①③④ |
设变量x,y满足:
,则z=|x-3y|的最大值为( )
|
| A、3 | ||
| B、8 | ||
C、
| ||
D、
|
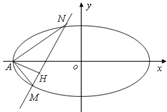 已知椭圆C:
已知椭圆C: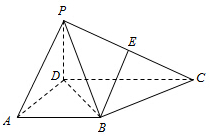 如图,在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,E为PC的中点,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=1,CD=2
如图,在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,E为PC的中点,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=1,CD=2