题目内容
7.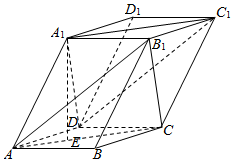 如图,棱柱ABCD-A1B1C1D1的底面是菱形.侧棱长为5,平面ABCD⊥平面A1ACC1,AB=3$\sqrt{3}$,∠BAD=60°,点E是△ABD的重心,且A1E=4.
如图,棱柱ABCD-A1B1C1D1的底面是菱形.侧棱长为5,平面ABCD⊥平面A1ACC1,AB=3$\sqrt{3}$,∠BAD=60°,点E是△ABD的重心,且A1E=4.(1)求证:平面A1DC1∥平面AB1C;
(2)求棱柱ABCD-A1B1C1D1的体积.
分析 (1)由AA1$\stackrel{∥}{=}$CC1得四边形A1ACC1是平行四边形,故A1C1∥AC.于是A1C1∥平面AB1C.同理可证DC1∥平面AB1C,故平面A1DC1∥平面AB1C;
(2)由等边三角形性质计算AE=3,由勾股定理的逆定理得出A1E⊥AC,从而A1E⊥平面ABCD,即A1E为棱柱的高.代入体积公式计算即可.
解答 (1)证明:∵AA1$\stackrel{∥}{=}$CC1,
∴四边形A1ACC1是平行四边形,
∴A1C1∥AC.∵AC?平面AB1C,A1C1?平面AB1C,
∴A1C1∥平面AB1C.
同理可证:DC1∥平面AB1C,
∵A1C1⊆平面A1DC1,DC1⊆平面A1DC1,A1C1∩DC1=C1,
∴平面A1DC1∥平面AB1C.
(2)解:连结BD,∵四边形ABCD是菱形,∠BAD=60°,
∴△ABD是等边三角形.
∵点E是△ABD的重心,AB=3$\sqrt{3}$,
∴AE=$\frac{2}{3}×\frac{\sqrt{3}}{2}AB$=3.又AA1=5,A1E=4,
∴$AA_1^2={A_1}{E^2}+A{E^2}$,即A1E⊥AC,
又∵平面ABCD⊥平面A1ACC1,平面ABCD∩平面A1ACC1=AC,A1E⊆平面A1ACC1,
∴A1E⊥平面ABCD.
∵S菱形ABCD=2S△ABD=2×$\frac{1}{2}×3\sqrt{3}×3\sqrt{3}×sin60°$=$\frac{27\sqrt{3}}{2}$,
∴棱柱ABCD-A1B1C1D1的体积V=S菱形ABCD•A1E=54$\sqrt{3}$.
点评 本题考查了面面平行的判定,面面垂直的性质,棱柱的体积计算,属于中档题.

练习册系列答案
相关题目
2.设复数z1,z2在复平面内的点关于实轴对称,z1=1+i,则$\frac{z_1}{z_2}$=( )
| A. | -i | B. | i | C. | -1 | D. | 1 |
19.用反证法证明命题:“已知x∈R,a=x2-1,b=2x+2,则a,b中至少有一个不小于0”,反设正确的是( )
| A. | 假设a,b都不大于0 | B. | 假设a,b至多有一个大于0 | ||
| C. | 假设a,b都大于0 | D. | 假设a,b都小于0 |