题目内容
17.已知Sn是等差数列{an}的前n项和,且S8>S9>S7,给出下列四个命题:①d<0;
②S16<0;
③数列{Sn}中的最大项为S15;
④|a8|>|a9|.
其中正确命题有①④.
分析 由S8>S9,且S9=S8+a9,得到a9<0,由S8>S7,S8=S7+a8,得到a8>0,从而d=a9-a8<0;由S9>S7,得到a8+a9>0,得到S16=8(a8+a9)>0;由a8>0,a9<0,得数列{Sn}中的最大项为S8,;由8(a8+a9)>0,得|a8|>|a9|.
解答 解:∵S8>S9,且S9=S8+a9,
∴S8>S8+a9,即a9<0,
又S8>S7,S8=S7+a8,
∴S7+a8>S7,即a8>0,
∴d=a9-a8<0,故①为真命题;
∵S9>S7,S9=S7+a8+a9,
∴S7+a8+a9>S7,即a8+a9>0,
又∵a1+a15=2a8,
∴S15=$\frac{15({a}_{1}+{a}_{15})}{2}$=15a8>0,
又∵a1+a16=a8+a9,
∴S16=$\frac{16({a}_{1}+{a}_{16})}{2}$=8(a8+a9)>0,故②错误;
又a1+a17=2a9,
∴S17=$\frac{17({a}_{1}+{a}_{17})}{2}$=17a9<0,
∵a8>0,a9<0,∴数列{Sn}中的最大项为S8,故③错误;
∵8(a8+a9)>0,∴|a8|>|a9|,故④正确;
故答案为:①④.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.已知复数z满足(1-i)z=2(i为虚数单位),则( )
| A. | |z|=2 | B. | z的实部为1 | ||
| C. | z的虚部为-1 | D. | z的共轭复数为1+i |
5.函数f(x)=sinωx(ω>0)在[-$\frac{π}{2}$,$\frac{π}{2}$]恰有11个零点,则ω的取值范围( )
| A. | [10,12) | B. | [16,20] | C. | [8,12] | D. | [12,14) |
12.已知角α是直线2x+y+1=0的倾斜角,那么tan(α-$\frac{π}{4}$)的值是( )
| A. | -$\frac{1}{3}$ | B. | -3 | C. | $\frac{1}{3}$ | D. | 3 |
9.已知F、A分别为双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的右焦点和右顶点,过F作x轴的垂线在第一象限与双曲线交于点P,AP的延长线与双曲线在第一象限的渐近线交于点Q,若$\overrightarrow{AP}$=(2-$\sqrt{2}}$)$\overrightarrow{AQ}$,则双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | $\sqrt{5}$ |
6.已知点A(1,0),B(2,3),向量$\overrightarrow{AC}$=(-3,-4),则向量$\overrightarrow{BC}$=( )
| A. | (-4,-7) | B. | (4,7) | C. | (4,-1) | D. | (4,1) |
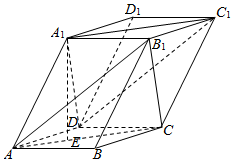 如图,棱柱ABCD-A1B1C1D1的底面是菱形.侧棱长为5,平面ABCD⊥平面A1ACC1,AB=3$\sqrt{3}$,∠BAD=60°,点E是△ABD的重心,且A1E=4.
如图,棱柱ABCD-A1B1C1D1的底面是菱形.侧棱长为5,平面ABCD⊥平面A1ACC1,AB=3$\sqrt{3}$,∠BAD=60°,点E是△ABD的重心,且A1E=4.