题目内容
19.用反证法证明命题:“已知x∈R,a=x2-1,b=2x+2,则a,b中至少有一个不小于0”,反设正确的是( )| A. | 假设a,b都不大于0 | B. | 假设a,b至多有一个大于0 | ||
| C. | 假设a,b都大于0 | D. | 假设a,b都小于0 |
分析 根据用反证法证明数学命题的方法和步骤,应先假设命题的否定成立,而要证明题的否定为:“假设a,b都小于0”,从而得出结论.
解答 解:根据用反证法证明数学命题的方法和步骤,应先假设命题的否定成立,
而命题:“已知x∈R,a=x2-1,b=2x+2,则a,b中至少有一个不小于0”的否定为“假设a,b都小于0”,
故选:D.
点评 本题主要考查用命题的否定,反证法证明数学命题的方法和步骤,把要证的结论进行否定,得到要证的结论的反面,是解题的突破口,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4. 省农科所经过5年对甲、乙两棉种的实验研究,将连续5年棉花产量(千克/亩)的统计数据用茎叶图表示如图,则平均产量较高与产量较稳定的分别是( )
省农科所经过5年对甲、乙两棉种的实验研究,将连续5年棉花产量(千克/亩)的统计数据用茎叶图表示如图,则平均产量较高与产量较稳定的分别是( )
 省农科所经过5年对甲、乙两棉种的实验研究,将连续5年棉花产量(千克/亩)的统计数据用茎叶图表示如图,则平均产量较高与产量较稳定的分别是( )
省农科所经过5年对甲、乙两棉种的实验研究,将连续5年棉花产量(千克/亩)的统计数据用茎叶图表示如图,则平均产量较高与产量较稳定的分别是( )| A. | 棉农甲;棉农甲 | B. | 棉农乙;棉农甲 | C. | 棉农甲;棉农乙 | D. | 棉农乙;棉农乙 |
11.函数f(x)的图象如图所示,则f(x)的极大值点的个数为( )


| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
8.已知复数z满足(1-i)z=2(i为虚数单位),则( )
| A. | |z|=2 | B. | z的实部为1 | ||
| C. | z的虚部为-1 | D. | z的共轭复数为1+i |
9.已知F、A分别为双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的右焦点和右顶点,过F作x轴的垂线在第一象限与双曲线交于点P,AP的延长线与双曲线在第一象限的渐近线交于点Q,若$\overrightarrow{AP}$=(2-$\sqrt{2}}$)$\overrightarrow{AQ}$,则双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | $\sqrt{5}$ |
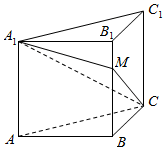 棱长为1的正方体ABCD-A1B1C1D1中,沿平面A1ACC1将正方体分成两部分,其中一部分如图所示,过直线A1C的平面A1CM与线段BB1交于点M.
棱长为1的正方体ABCD-A1B1C1D1中,沿平面A1ACC1将正方体分成两部分,其中一部分如图所示,过直线A1C的平面A1CM与线段BB1交于点M.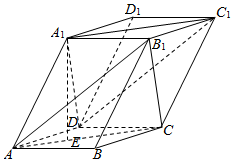 如图,棱柱ABCD-A1B1C1D1的底面是菱形.侧棱长为5,平面ABCD⊥平面A1ACC1,AB=3$\sqrt{3}$,∠BAD=60°,点E是△ABD的重心,且A1E=4.
如图,棱柱ABCD-A1B1C1D1的底面是菱形.侧棱长为5,平面ABCD⊥平面A1ACC1,AB=3$\sqrt{3}$,∠BAD=60°,点E是△ABD的重心,且A1E=4.