题目内容
17.如图(1),在等腰梯形ABCD中,AB∥CD,E,F分别为AB和CD的中点,且AB=EF=2,CD=6,M为EC中点,现将梯形ABCD沿EF所在直线折起,使平面EFCB⊥平面EFDA,如图(2)所示,N是CD的中点.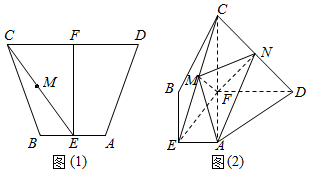
(Ⅰ)求证:MN∥平面ADFE;
(Ⅱ)求四棱锥M-EFDA的体积.
分析 (I)连接ED,由中位线性质得MN∥ED,故MN∥平面EFDA;
(II)由平面EFCB⊥平面EFDA可知CF⊥平面EFDA,由M为EC中点得棱锥M-EFDA的高为CF的一半.
解答 证明:(Ⅰ)连接ED,
∵M,N分别是EC,CD的中点,
∴MN∥ED,又MN?平面EFDA,ED?平面EFDA
∴MN∥平面EFDA.
(Ⅱ)∵平面EFDA⊥平面EFCB,平面EFDA∩平面EFCB=EF,CF⊥EF,CF?平面EFCB,
∴CF⊥平面EFDA,
∵M是EC的中点,
∴M到平面EFDA的距离h=$\frac{1}{2}$CF=$\frac{3}{2}$.
∴VM-EFDA=$\frac{1}{3}{S}_{梯形EFDA}•h$=$\frac{1}{3}×\frac{1}{2}×(1+3)×2×\frac{3}{2}$=2.
点评 本题考查了线面平行的判定,面面垂直的性质,棱锥的体积计算,属于基础题.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
7.以正方形的一条边的两个端点为焦点,且过另外两个顶点的椭圆与双曲线的离心率之积为( )
| A. | 1 | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
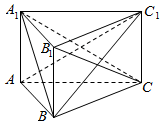 如图,在直三棱柱ABC-A1B1C1(侧棱垂直于底面的棱柱为直棱柱)中,BC=CC1=1,AC=2,∠ABC=90°.
如图,在直三棱柱ABC-A1B1C1(侧棱垂直于底面的棱柱为直棱柱)中,BC=CC1=1,AC=2,∠ABC=90°.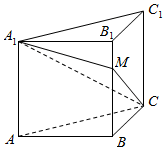 棱长为1的正方体ABCD-A1B1C1D1中,沿平面A1ACC1将正方体分成两部分,其中一部分如图所示,过直线A1C的平面A1CM与线段BB1交于点M.
棱长为1的正方体ABCD-A1B1C1D1中,沿平面A1ACC1将正方体分成两部分,其中一部分如图所示,过直线A1C的平面A1CM与线段BB1交于点M.
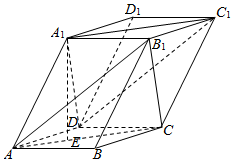 如图,棱柱ABCD-A1B1C1D1的底面是菱形.侧棱长为5,平面ABCD⊥平面A1ACC1,AB=3$\sqrt{3}$,∠BAD=60°,点E是△ABD的重心,且A1E=4.
如图,棱柱ABCD-A1B1C1D1的底面是菱形.侧棱长为5,平面ABCD⊥平面A1ACC1,AB=3$\sqrt{3}$,∠BAD=60°,点E是△ABD的重心,且A1E=4.