题目内容

5．顶点在原点，焦点在x轴上，且经过点P（-1，2）的拋物线的标准方程是（　　）
A．y2=$\frac{1}{4}$xB．y2=-$\frac{1}{4}$xC．y2=-4xD．x2=-4y

分析 利用抛物线的标准方程，通过点在抛物线上，求解即可．

解答 解：顶点在原点，焦点在x轴上，
设抛物线方程为：y2=mx，点P（-1，2）在拋物线上，可得：m=-4，
所求的抛物线方程为：y2=-4x．
故选：C．

点评 本题考查抛物线的简单性质，抛物线方程的求法，考查计算能力．

练习册系列答案
相关题目
13．已知等差数列{an}的前n项和为Sn，a4=9，S3=15．
（1）求Sn；
（2）设数列$\{\frac{1}{S_n}\}$的前n项和为Tn，证明：${T_n}＜\frac{3}{4}$．
16．已知$\frac{\overline z}{1+i}=2+i$，则复数z=（　　）
A．1-3iB．-1-3iC．-1+3iD．1+3i
13．关于x的方程$1-kx=\sqrt{1-{{（x-2）}^2}}$有实根时，k的取值范围是[-1，0]．
20．一个几何体的三视图如图所示，则该几何体的体积为（　　）
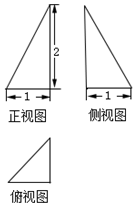
A．$\frac{1}{4}$B．$\frac{1}{3}$C．$\frac{2}{3}$D．1
10．设集合M={x|-3＜x＜2}，N={x∈Z|-1≤x≤3}，则M∩N等于（　　）
A．{0，1}B．{-1，0，1，2}C．{0，1，2}D．{-1，0，1}
17．执行如图所示的程序框图，则输出的x等于（　　）
A．16B．8C．4D．2
14．已知$sin（θ+\frac{π}{3}）=\frac{2}{3}$，则$cos（θ-\frac{π}{6}）$=$\frac{2}{3}$．
15．过正三棱柱底面一边所作的正三棱柱的截面是（　　）
A．三角形B．三角形或梯形
C．不是梯形的四边形D．梯形

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网