题目内容

1．（2x-3）4=a0+a1x+a2x2+a3x3+a4x4，求
（1）a1+a2+a3+a4．
（2）（a0+a2+a4）2-（a1+a3）2．

分析 （1）令x=1得（2-3）4=a0+a1+a2+a3+a4，令x=0得（0-3）4=a0，即可求出答案，
（2）令x=1得（2-3）4=a0+a1+a2+a3+a4．①，令x=-1得（-2-3）4=a0-a1+a2-a3+a4．②而（a0+a2+a4）2-（a1+a3）2，代值计算即可．（a0-a1+a2-a3+a4）（a0+a1+a2+a3+a4）

解答 解：（1）由（2x-3）4=a0+a1x+a2x2+a3x3+a4x4，
令x=1得（2-3）4=a0+a1+a2+a3+a4，
令x=0得（0-3）4=a0，
所以a1+a2+a3+a4=a0+a1+a2+a3+a4-a0=（2-3）4-81=-80．
（2）在（2x-3）4=a0+a1x+a2x2+a3x3+a4x4中，
令x=1得（2-3）4=a0+a1+a2+a3+a4．①
令x=-1得（-2-3）4=a0-a1+a2-a3+a4．②
所以由①②有（a0+a2+a4）2-（a1+a3）2
=（a0-a1+a2-a3+a4）（a0+a1+a2+a3+a4）
=（-2-3）4（2-3）4=（2+3）4（2-3）4=625．

点评 本题主要考查了二项展开式中利用赋值法求解二项展开式的各项系数之和（注意是各项系数之和，要区别于二项式系数之和），解饿答本题还要注意所求式子的特点：符合平方差公式．

练习册系列答案
相关题目
11．已知椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{2}}{2}$，点P（1，$\frac{\sqrt{2}}{2}$）在椭圆E上，直线l过椭圆的右焦点F且与椭圆相交于A，B两点．
（1）求E的方程；
（2）在x轴上是否存在定点M，使得$\overrightarrow{MA}$•$\overrightarrow{MB}$为定值？若存在，求出定点M的坐标；若不存在，说明理由．
12．在复平面xOy内，若A（2，-1），B（0，3），则?OACB中，点C对应的复数为（　　）
A．2+2iB．2-2iC．1+iD．1-i
9．设函数f（x）在点x0附近有定义，且有f（x0+△x）-f（x0）=a△x+b（△x）2，其中a，b为常数，则（　　）
A．f'（x）=aB．f'（x）=bC．f'（x0）=aD．f'（x0）=b
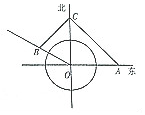16．某化工厂O正东方向和北偏西60°方向分别有两条通向工厂的公路，工厂正北方向有一观察站C，OC=2千米，因化工厂原料泄漏，工厂周围1千米的范围内均有不同程度的影响．现准备从观察站C处修两条隔离绿化带CA，CB（其中A，B为隔离带与公路交接点）．且使CA⊥CB，隔离带与两条公路线围成的面积为S．
（1）①若OA=a千米，试把S表示成a的函数．并写出其定义域；
②若∠OAC=θ，试把S表示成θ的函数，并写出其定义域；
（2）选择上述两个函数中的以个，试求S的最小值．
6．设直线x-y-a=0与圆x2+y2=4相交于A，B两点，O为坐标原点，若△AOB为等边三角形，则实数a的值为（　　）
A．$±\sqrt{3}$B．$±\sqrt{6}$C．±3D．±9
13．已知等差数列{an}的前n项和为Sn，a4=9，S3=15．
（1）求Sn；
（2）设数列$\{\frac{1}{S_n}\}$的前n项和为Tn，证明：${T_n}＜\frac{3}{4}$．
12．若函数f（x）满足f（2x-1）=x+1，则f（3）等于（　　）
A．3B．4C．5D．6
13．关于x的方程$1-kx=\sqrt{1-{{（x-2）}^2}}$有实根时，k的取值范围是[-1，0]．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网