题目内容
19.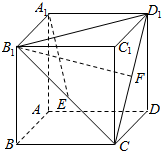 如图所示,正方体ABCD-A1B1C1D1中,E,F分别为侧面BB1C1C与CC1D1D的中心.
如图所示,正方体ABCD-A1B1C1D1中,E,F分别为侧面BB1C1C与CC1D1D的中心.(1)判断A1E与B1F的位置关系;
(2)求A1E与B1F所成的角的余弦值.
分析 (1)以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法得到A1E与B1F异面.
(2)设A1E与B1F所成的角为θ,由$\overrightarrow{{A}_{1}E}$=(-1,2,-1),$\overrightarrow{{B}_{1}F}$=(-2,-1,-1),利用向量法能求出A1E与B1F所成的角的余弦值.
解答 解:(1)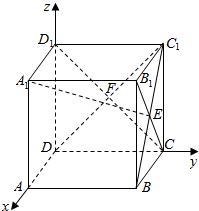 以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
设正方体ABCD-A1B1C1D1中棱长为2,
则E(1,2,1),A1(2,0,2),B1(2,2,2),F(0,1,1),
$\overrightarrow{{A}_{1}E}$=(-1,2,-1),$\overrightarrow{{B}_{1}F}$=(-2,-1,-1),
∴$\overrightarrow{{A}_{1}E}$与$\overrightarrow{{B}_{1}F}$不共线,又A1E与B1F没有交点,
∴A1E与B1F异面.
(2)设A1E与B1F所成的角为θ,
∵$\overrightarrow{{A}_{1}E}$=(-1,2,-1),$\overrightarrow{{B}_{1}F}$=(-2,-1,-1),
∴cosθ=$\frac{|\overrightarrow{{A}_{1}E}•\overrightarrow{{B}_{1}F}|}{|\overrightarrow{{A}_{1}E}|•|\overrightarrow{{B}_{1}F}|}$=$\frac{|2-2+1|}{\sqrt{4}•\sqrt{4}}$=$\frac{1}{4}$,
∴A1E与B1F所成的角的余弦值为$\frac{1}{4}$.
点评 本题考查空间中两条直线的位置关系的判断,考查两直线所成角的余弦值的求法,是基础题,解题时要认真审题,注意向量法的合理运用.

| A. | ?x>1,x+$\frac{1}{x}$≤2 | B. | ?x>1,x+$\frac{1}{x}$≤2 | C. | ?x≤1,x+$\frac{1}{x}$≤2 | D. | ?x≤1,x+$\frac{1}{x}$≤2 |
| A. | f(x)=$\frac{{x}^{2}-1}{x-1}$与g(x)=x+1 | B. | f(x)=lnex与g(x)=elnx | ||
| C. | f(x)=|x|与g(x)=$\sqrt{{x}^{2}}$ | D. | f(x)=$\sqrt{x-1}$•$\sqrt{x+1}$与g(x)=$\sqrt{{x}^{2}-1}$ |
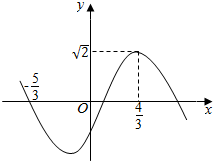 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的部分图象如图所示.
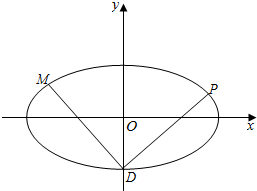 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{2\sqrt{2}}{3}$,椭圆C的右焦点到右准线的距离为$\frac{\sqrt{2}}{4}$,椭圆C的下顶点为D.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{2\sqrt{2}}{3}$,椭圆C的右焦点到右准线的距离为$\frac{\sqrt{2}}{4}$,椭圆C的下顶点为D.