题目内容
3.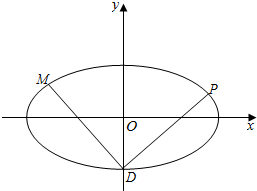 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{2\sqrt{2}}{3}$,椭圆C的右焦点到右准线的距离为$\frac{\sqrt{2}}{4}$,椭圆C的下顶点为D.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{2\sqrt{2}}{3}$,椭圆C的右焦点到右准线的距离为$\frac{\sqrt{2}}{4}$,椭圆C的下顶点为D.(1)求椭圆C的方程;
(2)若过D点作两条互相垂直的直线分别与椭圆C相交于点P、M.求证:直线PM经过一定点.
分析 (1)由题意可得c2=$\frac{8}{9}$a2,又$\frac{{a}^{2}}{c}$-c=$\frac{\sqrt{2}}{4}$,且a2=b2+c2,解得b=1,则a=3,即可得解椭圆C的方程;
(2)设直线PD的斜率为k,由$\left\{\begin{array}{l}{y=kx-1}\\{\frac{{x}^{2}}{9}+{y}^{2}=1}\end{array}\right.$得P($\frac{18k}{9{k}^{2}+1}$,$\frac{9{k}^{2}-1}{9{k}^{2}+1}$),M($\frac{-18k}{{k}^{2}+9}$,$\frac{9-{k}^{2}}{{k}^{2}+9}$),作直线l关于y轴的对称直线l′,可知定点在y轴上,当k=1时,P($\frac{9}{5}$,$\frac{4}{5}$),M(-$\frac{9}{5}$,$\frac{4}{5}$),可求此时直线PM经过y轴上的点T(0,$\frac{4}{5}$),证明kPT=kMT,即可得解P,M,T三点共线,即直线PM经过点T.
解答 解:(1)依题意知 e=$\frac{c}{a}=\frac{2\sqrt{2}}{3}$,则c2=$\frac{8}{9}$a2,…(2分)
又$\frac{{a}^{2}}{c}$-c=$\frac{\sqrt{2}}{4}$,且a2=b2+c2,
∴b=1,则a=3,
∴方程为$\frac{{x}^{2}}{9}$+y2=1.…(5分)
(2)由题意知直线PD,MD的斜率存在且不为0,设直线PD的斜率为k,则PD:y=kx-1,
由$\left\{\begin{array}{l}{y=kx-1}\\{\frac{{x}^{2}}{9}+{y}^{2}=1}\end{array}\right.$得P($\frac{18k}{9{k}^{2}+1}$,$\frac{9{k}^{2}-1}{9{k}^{2}+1}$),…(7分)
用-$\frac{1}{k}$去代k,得M($\frac{-18k}{{k}^{2}+9}$,$\frac{9-{k}^{2}}{{k}^{2}+9}$),…(9分)
作直线l关于y轴的对称直线l′,此时得到的点P′、M′关于y轴对称,
则PM与P′M′相交于y轴,可知定点在y轴上,当k=1时,P($\frac{9}{5}$,$\frac{4}{5}$),M(-$\frac{9}{5}$,$\frac{4}{5}$),
此时直线PM经过y轴上的点T(0,$\frac{4}{5}$),…(10分)
∵kPT=$\frac{\frac{9{k}^{2}-1}{9{k}^{2}+1}-\frac{4}{5}}{\frac{18k}{9{k}^{2}+1}}=\frac{{k}^{2}-1}{10k}$,…(12分)
kMT=$\frac{\frac{9-{k}^{2}}{{k}^{2}+9}-\frac{4}{5}}{-\frac{18k}{{k}^{2}+9}}$=$\frac{{k}^{2}-1}{10k}$ …(14分)
∴kPT=kMT,
∴P,M,T三点共线,即直线PM经过点T,
故直线PM经过定点T(0,$\frac{4}{5}$).…(15分)
点评 本题考查椭圆方程的求法,考查直线是否过定点的判断与求法,解题时要认真审题,注意函数与方程思想的合理运用,属于中档题.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案| A. | [-1,5] | B. | [0,3] | C. | [-$\sqrt{3}$,$\sqrt{3}$] | D. | [1,49] |
| A. | k=$\frac{1}{e}$+e | |
| B. | 函数f(x)的图象在点(0,f(0))处的切线的斜率为e2-$\frac{1}{e}$ | |
| C. | 函数f(x)在[0,e]上单调递减 | |
| D. | 函数f(x)在[0,e]上的最大值为2e3+1 |
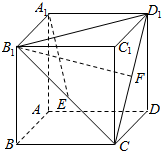 如图所示,正方体ABCD-A1B1C1D1中,E,F分别为侧面BB1C1C与CC1D1D的中心.
如图所示,正方体ABCD-A1B1C1D1中,E,F分别为侧面BB1C1C与CC1D1D的中心.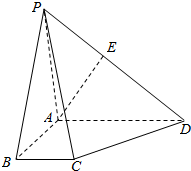 在四棱锥P-ABCD中,底面ABCD是一直角梯形,PA⊥底面ABCD,∠BAD=90°,AD∥BC,AB=BC=1,AD=AP=2,E是PD的中点.
在四棱锥P-ABCD中,底面ABCD是一直角梯形,PA⊥底面ABCD,∠BAD=90°,AD∥BC,AB=BC=1,AD=AP=2,E是PD的中点.