题目内容
10.已知定义域为R上的偶函数f(x)在[0,+∞)上单调递增,且f($\frac{1}{2}$)=0,则不等式f(x-2)>0的解集是{x|x>$\frac{5}{2}$或x<$\frac{3}{2}$}.分析 根据函数的奇偶性和单调性之间的关系,将不等式进行转化,即可得到不等式的解集.
解答 解:∵偶函数f(x)在[0,+∞)上为增函数,f($\frac{1}{2}$)=0,
∴不等式f(x-2)>0等价为f(|x-2|)>f($\frac{1}{2}$),
即|x-2|>$\frac{1}{2}$,
即x-2>$\frac{1}{2}$或x-2<-$\frac{1}{2}$,
即x>$\frac{5}{2}$或x<$\frac{3}{2}$,
∴不等式f(x-2)>0的解集为{x|x>$\frac{5}{2}$或x<$\frac{3}{2}$}.
故答案为:{x|x>$\frac{5}{2}$或x<$\frac{3}{2}$}.
点评 本题主要考查不等式的解法和应用问题,解题时应利用函数的奇偶性和单调性之间的关系进行等价转化,是综合性题目.

练习册系列答案
相关题目
1.若函数f(x)=x1g(mx+$\sqrt{{x}^{2}+1}$)为偶函数,则m=( )
| A. | -1 | B. | 1 | C. | -1或1 | D. | 0 |
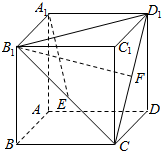 如图所示,正方体ABCD-A1B1C1D1中,E,F分别为侧面BB1C1C与CC1D1D的中心.
如图所示,正方体ABCD-A1B1C1D1中,E,F分别为侧面BB1C1C与CC1D1D的中心.