题目内容
14.如图,在复平面内,点A对应的复数为z1,若$\frac{{z}_{2}}{{z}_{1}}$=i(i为虚数单位),则z2=-2-i.
分析 由图求得z1,代入$\frac{{z}_{2}}{{z}_{1}}$=i后利用复数代数形式的乘法运算得答案.
解答 解:由图可得,z1=-1+2i,
∴由$\frac{{z}_{2}}{{z}_{1}}$=i,得z2=z1i=(-1+2i)•i=-2-i.
故答案为:-2-i.
点评 本题考查复数的代数表示法及其几何意义,考查复数代数形式的乘除运算,是基础题.

练习册系列答案
相关题目
4.变量x,y具有线性相关关系,现测得一组数据如下:
根据如表,利用最小二乘法得到回归直线方程$\stackrel{∧}{y}$=0.7x+0.55,据此判断,当x=5,时,$\stackrel{∧}{y}$与实际值y的大小关系为( )
| x | 2 | 3 | 4 | 5 |
| y | 2 | 2.5 | 3.5 | 4 |
| A. | $\stackrel{∧}{y}$>y | B. | $\stackrel{∧}{y}$>y | C. | $\stackrel{∧}{y}$=y | D. | 无法确定 |
3.在△ABC中,已知(a2-b2)sin(A+B)=(a2+b2)sin(A-B),(A≠B),则△ABC是( )
| A. | 等腰三角形 | B. | 直角三角形 | ||
| C. | 等腰直角三角形 | D. | 等腰或直角三角形 |
4.已知函数f(x)=x3+kx(k∈R),若关于x的方程f(x)=lnx+2ex2有唯一解,则下列说法正确的是( )
| A. | k=$\frac{1}{e}$+e | |
| B. | 函数f(x)的图象在点(0,f(0))处的切线的斜率为e2-$\frac{1}{e}$ | |
| C. | 函数f(x)在[0,e]上单调递减 | |
| D. | 函数f(x)在[0,e]上的最大值为2e3+1 |
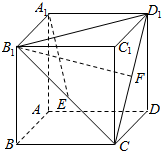 如图所示,正方体ABCD-A1B1C1D1中,E,F分别为侧面BB1C1C与CC1D1D的中心.
如图所示,正方体ABCD-A1B1C1D1中,E,F分别为侧面BB1C1C与CC1D1D的中心.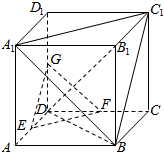 如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是AD、CD、DD1的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是AD、CD、DD1的中点.