题目内容
9.设命题p:?x>1,x+$\frac{1}{x}$>2,则¬p为( )| A. | ?x>1,x+$\frac{1}{x}$≤2 | B. | ?x>1,x+$\frac{1}{x}$≤2 | C. | ?x≤1,x+$\frac{1}{x}$≤2 | D. | ?x≤1,x+$\frac{1}{x}$≤2 |
分析 本题中的命题是一个全称命题,其否定是特称命题,依据全称命题的否定书写形式:将量词“?”与“?”互换,结论同时否定,写出命题的否定即可
解答 解:∵命题p:?x>1,x+$\frac{1}{x}$>2,
∴命题p的否定是“?x>1,x+$\frac{1}{x}$≤2”
故选:B.
点评 本题考查命题的否定,解题的关键是掌握并理解命题否定的书写方法规则,全称命题的否定是特称命题,特称命题的否定是全称命题,书写时注意量词的变化.

练习册系列答案
相关题目
19.△ABC的三个内角A,B,C对应的边分别为a,b,c,且asin($\frac{3π}{2}$-C),bcos(2π-B),ccos(π+A)成等差数列,则△ABC是( )
| A. | 直角三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 正三角形 |
4.变量x,y具有线性相关关系,现测得一组数据如下:
根据如表,利用最小二乘法得到回归直线方程$\stackrel{∧}{y}$=0.7x+0.55,据此判断,当x=5,时,$\stackrel{∧}{y}$与实际值y的大小关系为( )
| x | 2 | 3 | 4 | 5 |
| y | 2 | 2.5 | 3.5 | 4 |
| A. | $\stackrel{∧}{y}$>y | B. | $\stackrel{∧}{y}$>y | C. | $\stackrel{∧}{y}$=y | D. | 无法确定 |
1.若函数f(x)=x1g(mx+$\sqrt{{x}^{2}+1}$)为偶函数,则m=( )
| A. | -1 | B. | 1 | C. | -1或1 | D. | 0 |
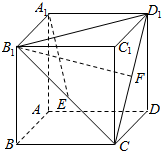 如图所示,正方体ABCD-A1B1C1D1中,E,F分别为侧面BB1C1C与CC1D1D的中心.
如图所示,正方体ABCD-A1B1C1D1中,E,F分别为侧面BB1C1C与CC1D1D的中心.