题目内容
2.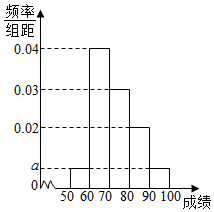 某校100名学生其中考试数学成绩的频率分布直方图如图所示,其中成绩分布区间是[50,60),[60,70),[70,80),[80,90),[90,100].
某校100名学生其中考试数学成绩的频率分布直方图如图所示,其中成绩分布区间是[50,60),[60,70),[70,80),[80,90),[90,100].(1)求图中a的值;
(2)根据频率分布直方图,估计这次100名学生数学成绩的平均数及中位数.
分析 (1)根据频率和为1,列出方程求出a的值;
(2)根据频率分布直方图计算出平均数与中位数的值.
解答 解:(1)由频率分布直方图可知:
2a+0.04+0.03+0.02=0.1,
所以a=0.005;
(2)根据频率分布直方图,估计平均数为:
55×0.05+65×0.4+75×0.3+85×0.2+95×0.05=73(分).
估计中位数为:
70+$\frac{0.05}{0.3}$×10=$\frac{215}{3}$(分).
点评 本题考查了频率分布直方图的应用问题,也考查了平均数与中位数的计算问题,是基础题目.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
12.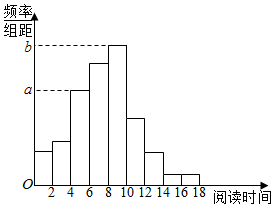 从某校随机抽取200名学生,获得了他们的一周课外阅读时间(单位:小时)的数据,整理得到数据分组级频数分布直方图:
从某校随机抽取200名学生,获得了他们的一周课外阅读时间(单位:小时)的数据,整理得到数据分组级频数分布直方图:
(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的概率;
(2)求频率分布直方图中的a,b的值;
(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的200名学生该周课外阅读时间的平均数在第几组.
 从某校随机抽取200名学生,获得了他们的一周课外阅读时间(单位:小时)的数据,整理得到数据分组级频数分布直方图:
从某校随机抽取200名学生,获得了他们的一周课外阅读时间(单位:小时)的数据,整理得到数据分组级频数分布直方图:| 编号 | 分组 | 频数 |
| 1 | [0,2) | 12 |
| 2 | [2,4) | 16 |
| 3 | [4,6) | 34 |
| 4 | [6,8) | 44 |
| 5 | [8,10) | 50 |
| 6 | [10,12) | 24 |
| 7 | [12,14) | 12 |
| 8 | [14,16) | 4 |
| 9 | [16,18) | 4 |
| 合计 | 200 | |
(2)求频率分布直方图中的a,b的值;
(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的200名学生该周课外阅读时间的平均数在第几组.
11.过原点的一条直线与双曲线C1:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)交于A,B两点,P为双曲线上不同于A,B的一个动点,且直线PA、PB的斜率之积为3,若抛物线C2:y2=2px(p>0)的焦点到双曲线C1的渐近线的距离为2,则该抛物线C2的标准方程为( )
| A. | y2=$\frac{16\sqrt{3}}{3}$x | B. | y2=16x | C. | y2=$\frac{8\sqrt{3}}{3}$x | D. | y2=8x |
12.若函数f(x)=b+lg($\sqrt{{x}^{2}+1}$-ax)是定义在R上的奇函数,则a+b=( )
| A. | -1 | B. | 0 | C. | -1或1 | D. | 0或2 |