题目内容
12.若函数f(x)=b+lg($\sqrt{{x}^{2}+1}$-ax)是定义在R上的奇函数,则a+b=( )| A. | -1 | B. | 0 | C. | -1或1 | D. | 0或2 |
分析 由于f(x)为定义在R上的奇函数,则f(0)=0,可得b=0,再运用定义,求出a,即可求出a+b的值.
解答 解:由于f(x)为定义在R上的奇函数,
则f(0)=0,即有b+lg1=0,
解得:b=0.
则有f(x)=lg($\sqrt{{x}^{2}+1}$-ax),
f(-x)+f(x)=lg($\sqrt{{x}^{2}+1}$+ax)+lg($\sqrt{{x}^{2}+1}$-ax)=lg(x2+1-a2x2)=lg1=0,
可得a2=1,解得a=±1.
a+b=±1.
故选:C.
点评 本题考查函数的奇偶性的判断,考查定义法和奇偶性的性质的运用,考查运算能力,属于中档题.

练习册系列答案
相关题目
4.已知定义在R内的奇函数f(x)满足:对任意x∈R郡有f(x+1)=f(3-x),若f(1)=-2,则2016f(2016)-2015f(2015)=( )
| A. | -2015 | B. | 2015 | C. | -4030 | D. | 4030 |
2.已知集合P={(x,y)|$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)},Q={(x,y)|$\frac{x}{a}$+$\frac{y}{b}$>m(a>b>0,m>0)},若?M∈P,M∉Q,则实数m的取值范围是( )
| A. | [$\sqrt{2}$,+∞) | B. | [2$\sqrt{2}$,+∞) | C. | [$\frac{\sqrt{6}}{6}$,+∞) | D. | (-∞,0] |
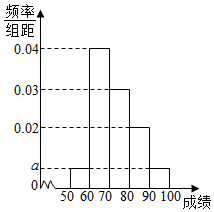 某校100名学生其中考试数学成绩的频率分布直方图如图所示,其中成绩分布区间是[50,60),[60,70),[70,80),[80,90),[90,100].
某校100名学生其中考试数学成绩的频率分布直方图如图所示,其中成绩分布区间是[50,60),[60,70),[70,80),[80,90),[90,100].