题目内容
17．直线y=2x+m与椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1有两个公共点，则实数m的取值范围是（-2$\sqrt{10}$，2$\sqrt{10}$）．分析 直线与椭圆联立，消去y后得到一个关于x的一元二次方程，由直线与椭圆有一两个交点，利用根的判别式能求出m的取值范围．
解答 解：联立$\left\{\begin{array}{l}{y=2x+m}\\{\frac{{x}^{2}}{9}+\frac{{y}^{2}}{4}=1}\end{array}\right.$，消去y，
得：40x2+36mx+9m2-36=0，
∵直线y=2x+m与椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1有两个公共点，
∴△=（36m）2-4×40×（9m2-36）＞0，
解得-2$\sqrt{10}＜m＜2\sqrt{10}$．
∴实数m的取值范围是（-2$\sqrt{10}$，2$\sqrt{10}$）．
故答案为：（-2$\sqrt{10}$，2$\sqrt{10}$）．
点评 本题考查实数的取值范围的求法，是中档题，解题时要认真审题，注意根的判别式的合理运用．
练习册系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
7．设全集U={-2，-1，0，1，2}，集合M={-1，0，1}，N={x|x2-x-2=0}，则（∁UM）∩N=（ ）
| A． | {2} | B． | {-1} | C． | {-2，-1，2} | D． | {-1，1} |
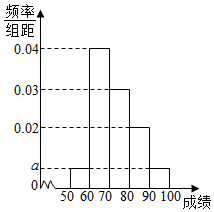某校100名学生其中考试数学成绩的频率分布直方图如图所示，其中成绩分布区间是[50，60），[60，70），[70，80），[80，90），[90，100]．