题目内容
已知定义在R上的偶函数y=f(x)满足:①f(x)=f(2-x);②当0≤x≤1时,f(x)=x2
(1)求f(5.5)的值;
(2)证明:x∈R时,f(x+2)=f(x)
(1)求f(5.5)的值;
(2)证明:x∈R时,f(x+2)=f(x)
考点:抽象函数及其应用,函数的周期性
专题:函数的性质及应用
分析:(1)由偶函数y=f(x)和①f(x)=f(2-x)推出函数的周期为2,将f(5.5)转化为f(0.5),再由条件②,即可得到结果;
(2)运用偶函数y=f(x)和①f(x)=f(2-x)即可推出函数的周期为2.
(2)运用偶函数y=f(x)和①f(x)=f(2-x)即可推出函数的周期为2.
解答:
(1)解:∵f(x)=f(2-x)
即f(-x)=f(2+x)
又∵f(x)为偶函数,
∴f(-x)=f(x)
∴f(x+2)=f(x)
∴f(x)是周期为2的函数.
∴f(5.5)=f(5.5-6)=f(-0.5)=f(0.5)
又0≤x≤1时 f(x)=x2
∴f(0.5)=
即f(5.5)=
;
(2)证明:∵f(x)=f(2-x)
即f(-x)=f(2+x)
又∵f(x)为偶函数,
∴f(-x)=f(x)
∴f(x+2)=f(x).
即x∈R时,f(x+2)=f(x).
即f(-x)=f(2+x)
又∵f(x)为偶函数,
∴f(-x)=f(x)
∴f(x+2)=f(x)
∴f(x)是周期为2的函数.
∴f(5.5)=f(5.5-6)=f(-0.5)=f(0.5)
又0≤x≤1时 f(x)=x2
∴f(0.5)=
| 1 |
| 4 |
| 1 |
| 4 |
(2)证明:∵f(x)=f(2-x)
即f(-x)=f(2+x)
又∵f(x)为偶函数,
∴f(-x)=f(x)
∴f(x+2)=f(x).
即x∈R时,f(x+2)=f(x).
点评:本题考查函数的周期性和奇偶性及其运用,同时考查解决抽象函数的常用方法:赋值或赋式,应掌握.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
已知函数f(x)的导数为f′(x),且满足f(x)=3x2+2xf′(2),则f′(5)=( )
| A、6 | B、7 | C、8 | D、9 |
在△ABC中,sinC=2sinAcosB,则△ABC的形状为( )
| A、直角三角形 |
| B、等腰三角形 |
| C、等腰直角三角形 |
| D、不能确定 |
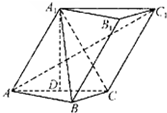 已知三棱柱ABC-A1B1C1中,∠BCA=90°,AA1=AC=BC=2,A1在底面ABC上的射影恰为AC的中点D.
已知三棱柱ABC-A1B1C1中,∠BCA=90°,AA1=AC=BC=2,A1在底面ABC上的射影恰为AC的中点D.