题目内容
数列{an}满足:a1=1,an+1=
+1,n∈N*.
(Ⅰ)写出a2,a3,a4,猜想通项公式an,用数学归纳法证明你的猜想;
(Ⅱ)求证:
+
+…+
<
(an+1)2,n∈N*.
| n2an+an2 |
| an2+2an-n |
(Ⅰ)写出a2,a3,a4,猜想通项公式an,用数学归纳法证明你的猜想;
(Ⅱ)求证:
| a 1a2 |
| a2a3 |
| ana n+1 |
| 1 |
| 2 |
考点:数列递推式,数列与不等式的综合
专题:等差数列与等比数列
分析:(Ⅰ)由已知条件,利用递推公式能求出a2=2,a3=3,a4=4,由此猜想an=n,再用数学归纳法证明.
(Ⅱ)an=n,知证明
+
+…+
<
(an+1)2,n∈N*.即证
+
+…+
<
(n+1)2,由此利用均值定理能求出来.
(Ⅱ)an=n,知证明
| a 1a2 |
| a2a3 |
| ana n+1 |
| 1 |
| 2 |
| 1×2 |
| 2×3 |
| n×(n+1) |
| 1 |
| 2 |
解答:
解:(Ⅰ)∵数列{an}满足:a1=1,an+1=
+1,n∈N*.
∴a2=
+1=2,
a3=
+1=3,
a4=
+1=4,猜想an=n
证明:①当n=1时,a1=1,猜想成立;
②假设当n=k(k∈N*)时猜想成立,即ak=k
那么,ak+1=
+1=k+1,
∴当n=k+1时猜想也成立
由①②可知猜想对任意n∈N*都成立,即an=n
(Ⅱ)证明:∵an=n,
证明
+
+…+
<
(an+1)2,n∈N*.
即证
+
+…+
<
(n+1)2
由均值不等式知:
<
=n+
,
则
+
+…+
<(1+2+…+n)+
=
+
=
<
(n+1)2.
∴
+
+…+
<
(an+1)2,n∈N*.
| n2an+an2 |
| an2+2an-n |
∴a2=
| 1+1 |
| 1+2-1 |
a3=
| 4×2+4 |
| 4+4-2 |
a4=
| 9×3+9 |
| 9+6-3 |
证明:①当n=1时,a1=1,猜想成立;
②假设当n=k(k∈N*)时猜想成立,即ak=k
那么,ak+1=
| k2•k+k2 |
| k2+2k-k |
∴当n=k+1时猜想也成立
由①②可知猜想对任意n∈N*都成立,即an=n
(Ⅱ)证明:∵an=n,
证明
| a 1a2 |
| a2a3 |
| ana n+1 |
| 1 |
| 2 |
即证
| 1×2 |
| 2×3 |
| n×(n+1) |
| 1 |
| 2 |
由均值不等式知:
| n×(n+1) |
| n+n+1 |
| 2 |
| 1 |
| 2 |
则
| 1×2 |
| 2×3 |
| n×(n+1) |
| n |
| 2 |
| n(n+1) |
| 2 |
| n |
| 2 |
| n(n+2) |
| 2 |
| 1 |
| 2 |
∴
| a 1a2 |
| a2a3 |
| ana n+1 |
| 1 |
| 2 |
点评:本题考查数列的通项公式的求法,考查不等式的证明,解题时要认真审题,注意数学归纳法的合理运用.

练习册系列答案
相关题目
已知条件p:x<2,条件q:x<3,则p是q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
“a>b”是“log3a>log3b”的( )条件.
| A、充分不必要 |
| B、必要不充分 |
| C、充要 |
| D、既不充分也不必要 |
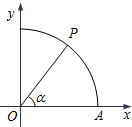 如图,曲线Γ:x2+y2=1(x≥0,y≥0)与x轴交于点A,点P在曲线Γ上,∠AOP=α.
如图,曲线Γ:x2+y2=1(x≥0,y≥0)与x轴交于点A,点P在曲线Γ上,∠AOP=α.