题目内容

求圆心在C（2，-1），且截直线y=x-1所得的弦长为2
2
的圆的方程．
考点：圆的标准方程
专题：直线与圆
分析：由条件求出弦心距，再利用弦长公式求出半径，即可求得圆的标准方程．
解答： 解：设半径为r，由于弦长l=2
2
，弦心距d=
|2-(-1)-1|
2
=
2
，
∴r=
d2+(
l
2
)2
=
2+2
=2，故圆的方程为 （x-2）2+（y+1）2=4．
点评：本题主要考查直线和圆的位置关系，求圆的标准方程，点到直线的距离公式，弦长公式的应用，属于基础题．
练习册系列答案
相关题目
若定义在R上奇函数f（x）满足f（x）=f（x+5），且f（1）=1，则f（4）=（　　）
A、-1B、1C、-2D、2
若函数y=f（x）的定义域为（-∞，0）∪（0，+∞），对定义域内的任意两个实数x，y，都有f（xy）=f（x）+f（y），并且当x＞1时，f（x）＞0，且f（4）=2
（1）证明函数y=f（x）为偶函数；
（2）证明函数f（x）在（0，+∞）上为增函数；
（3）若函数g（x）=2x-2，且当a∈[1，4]时，有f（a）=g（b），求b的取值范围．
已知定义在R上的偶函数y=f（x）满足：①f（x）=f（2-x）；②当0≤x≤1时，f（x）=x2
（1）求f（5.5）的值；
（2）证明：x∈R时，f（x+2）=f（x）
已知函数f(x)=ln(x+
3
2
)+
2
x
，g（x）=
1
x2-1
+a；
（1）求函数f（x）的单调区间；
（2）若方程g（x）=ln（x2+1）有4个不同的实根，求a的范围？
（3）是否存在正数b，使得关于x的方程f（x）=blnx有两个不相等的实根？如果存在，求b满足的条件，如果不存在，说明理由．
若M≥
|ab(a2-b2)+bc(b2-c2)+ca(c2-a2)|
a2+b2+c2
对一切实数a、b、c都成立，求最小的实数M．
某软件公司研发了多款软件，其中A，B，C三种软件供高中生使用，经某高中使用一学年后，该公司调查了这个学校同一年级四个班的使用情况，从各班抽取的样本人数如下表：
班级 一 二 三 四
人数 3 2 3 4
（1）从这12人中随机抽取2人，求这2人恰好来自同一个班级的概率；
（2）从这12人中，指定甲、乙、丙3人为代表，已知他们每人选择一款软件，其中选A，B两款软件的概率都是
1
6
，且他们选择A，B，C任一款软件都是相互独立的．设这3名学生中选择软件C的人数为ξ，求ξ的分布列和数学期望．
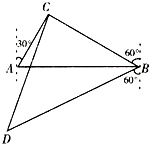某海域设立东西方向两个观测点A、B，相距
20
3
3
海里．现接到一艘渔船发出的求救讯号，测出该船位于点A北偏东30°，点B北偏西60°的C点．立刻通知位于B观测点南偏西60°且与B点相距16海里的D处的救援船前去营救，若救援船以28海里/小时的航速前往，问需要多长时间到达C处？
已知A（2，0），B（5，9），动点D满足条件：
OD
=t
OA
+（1-t）
OB
，t∈R．
（1）求动点D的轨迹的参数方程（以t为参数）；
（2）动点D的轨迹与抛物线y2=9x相交于P，Q两点，求线段PQ中点M的坐标．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网