题目内容
已知数列{an}的前n项和Sn=n3-10n2(?n∈N*).
(1)求an;
(2)求集合{n|an<0,n∈N*}(用列举法表示).
(1)求an;
(2)求集合{n|an<0,n∈N*}(用列举法表示).
考点:数列递推式
专题:等差数列与等比数列
分析:(1)由an=
,由此能求出an.
(2)方法一:由(1)得an=3n2-23n+11<0,从而得到
<n<
,由此能求出集合{n|an<0,n∈N*}.
(2)方法二:设f(x)=x3-10x2,x∈[1,+∞),利用导数性质能求出集合{n|an<0,n∈N*}.
|
(2)方法一:由(1)得an=3n2-23n+11<0,从而得到
23-
| ||
| 2×3 |
23+
| ||
| 2×3 |
(2)方法二:设f(x)=x3-10x2,x∈[1,+∞),利用导数性质能求出集合{n|an<0,n∈N*}.
解答:
解:(1)n=1时,a1=S1=-9…(1分),
n>1时,an=Sn-Sn-1=n3-10n2-[(n-1)3-10(n-1)2]
=3n2-23n+11,…(5分)
n=1时,3n2-23n+11=-9,…(6分)
?n∈N*,an=3n2-23n+11.…(7分)
(2)方法一:由(1)得an=3n2-23n+11<0,…(8分)
<n<
…(10分)
∵?n∈N*,∴1≤n≤7,…(12分)
∴所求集合{n|an<0,n∈N*}={1,2,3,4,5,6,7}.…(13分)
(2)方法二:设f(x)=x3-10x2,x∈[1,+∞),
则f′(x)=3x2-20x,…(10分)
由f′(x)=3x2-20x<0,得0<x<
,…(11分)
由0<n-1<
,
?n∈N*得n=2,3,4,5,6,7…(12分),
a1=S1=-9<0,a8=S8-S7=19>0,
∴{n|an<0,n∈N*}={1,2,3,4,5,6,7}.…(13分)
n>1时,an=Sn-Sn-1=n3-10n2-[(n-1)3-10(n-1)2]
=3n2-23n+11,…(5分)
n=1时,3n2-23n+11=-9,…(6分)
?n∈N*,an=3n2-23n+11.…(7分)
(2)方法一:由(1)得an=3n2-23n+11<0,…(8分)
23-
| ||
| 2×3 |
23+
| ||
| 2×3 |
∵?n∈N*,∴1≤n≤7,…(12分)
∴所求集合{n|an<0,n∈N*}={1,2,3,4,5,6,7}.…(13分)
(2)方法二:设f(x)=x3-10x2,x∈[1,+∞),
则f′(x)=3x2-20x,…(10分)
由f′(x)=3x2-20x<0,得0<x<
| 20 |
| 3 |
由0<n-1<
| 20 |
| 3 |
?n∈N*得n=2,3,4,5,6,7…(12分),
a1=S1=-9<0,a8=S8-S7=19>0,
∴{n|an<0,n∈N*}={1,2,3,4,5,6,7}.…(13分)
点评:本题考查数列的通项公式的求法,考查集合的求法,是中档题,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
相关题目
 如图,△A′O′B′是水平放置的△AOB由斜二测画法得到的直观图,则原△AOB的三边及中线AM中,最长的线段是( )
如图,△A′O′B′是水平放置的△AOB由斜二测画法得到的直观图,则原△AOB的三边及中线AM中,最长的线段是( )| A、AB | B、OB | C、AM | D、AO |
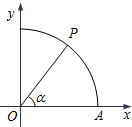 如图,曲线Γ:x2+y2=1(x≥0,y≥0)与x轴交于点A,点P在曲线Γ上,∠AOP=α.
如图,曲线Γ:x2+y2=1(x≥0,y≥0)与x轴交于点A,点P在曲线Γ上,∠AOP=α.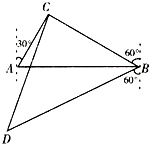 某海域设立东西方向两个观测点A、B,相距
某海域设立东西方向两个观测点A、B,相距