题目内容
已知直线a,b和平面α,β,γ,试判断下列说法是否正确,并说明理由:
(1)若a∥α,a∥b,b?α,则b∥α;
(2)若a∥β,β∥γ,则a∥γ;
(3)若a⊥α,b⊥a,b?α,则b∥α;
(4)若a⊥γ,β∥γ,则a⊥β.
(1)若a∥α,a∥b,b?α,则b∥α;
(2)若a∥β,β∥γ,则a∥γ;
(3)若a⊥α,b⊥a,b?α,则b∥α;
(4)若a⊥γ,β∥γ,则a⊥β.
考点:空间中直线与平面之间的位置关系
专题:空间位置关系与距离
分析:根据空间线面关系,线线关系,面面关系的定义,几何特征,性质及判定方法,逐一判断四个答案中的结论的真假,即可得到答案.
解答:
解:(1)若a∥α,a∥b,则b∥α或b?α,又由b?α,则b∥α,故(1)正确;
(2)若a∥β,β∥γ,则a∥γ或a?γ,故(2)错误;
(3)若a⊥α,b⊥a,则b∥α或b?α,又由b?α,则b∥α,故(3)正确;
(4)若a⊥γ,β∥γ,根据两个平行平面与同一直线的夹角相等可得:a⊥β,故(4)正确.
(2)若a∥β,β∥γ,则a∥γ或a?γ,故(2)错误;
(3)若a⊥α,b⊥a,则b∥α或b?α,又由b?α,则b∥α,故(3)正确;
(4)若a⊥γ,β∥γ,根据两个平行平面与同一直线的夹角相等可得:a⊥β,故(4)正确.
点评:本题考查的知识点是空间直线与平面之间的位置关系,熟练掌握空间线面关系,面面关系,线线关系的定义,几何特征及性质和判定方法是解答的关键.

练习册系列答案
相关题目
集合A={x|2≤x<4},B={x|x≥3},则A∩B=( )
| A、[2,4) |
| B、[3,+∞) |
| C、[3,4) |
| D、[2,3) |
已知某几何体的三视图(单位:dm)如图所示,则该几何体的体积是( )


A、
| ||
B、
| ||
| C、1dm3 | ||
D、
|
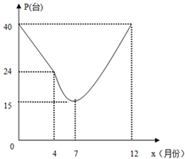 由于国家重点扶持节能环保产业,某种节能产品的市场销售回暖.某经销商销售这种产品,年初与生产厂家签订进货合同,约定一年内进价为0.1万元/台.一年后,实际月销售量P(台)与月次x之间存在如图所示函数关系(4月到12月近似符合二次函数关系).
由于国家重点扶持节能环保产业,某种节能产品的市场销售回暖.某经销商销售这种产品,年初与生产厂家签订进货合同,约定一年内进价为0.1万元/台.一年后,实际月销售量P(台)与月次x之间存在如图所示函数关系(4月到12月近似符合二次函数关系).