题目内容
设函数f(x)=1-x2+ln(x+1)
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若不等式f(x)>
-x2 (k∈N*)在(0,+∞)上恒成立,求k的最大值.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若不等式f(x)>
| kx |
| x+1 |
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)首先求出f(x)的定义域,函数f(x)的导数,分别令它大于0,小于0,解不等式,必须注意定义域,求交集;
(Ⅱ)化简不等式f(x)>
-x2,得:(x+1)[1+ln(x+1)]>kx,令g(x)=(x+1))[1+ln(x+1)]-kx,求出g'(x),由x>0,求出2+ln(x+1)>2,讨论k,分k≤2,k>2,由恒成立结合单调性判断k的取值,从而得到k的最大值.
(Ⅱ)化简不等式f(x)>
| kx |
| x+1 |
解答:
解:(Ⅰ)函数f(x)的定义域为(-1,+∞),
函数f(x)的导数f'(x)=-2x+
,
令f'(x)>0则
>2x,
解得
<x<
,
令f'(x)<0则
<2x,
解得x>
或x<
,
∵x>-1,
∴f(x)的单调增区间为(-1,
),
单调减区间为(
,+∞);
(Ⅱ)不等式f(x)>
-x2
即1-x2+ln(x+1)>
-x2,即1+ln(x+1)>
,
即(x+1)[1+ln(x+1)]>kx(k∈N*)在(0,+∞)上恒成立,
令g(x)=(x+1))[1+ln(x+1)]-kx,则
g'(x)=2+ln(x+1)-k,
∵x>0,∴2+ln(x+1)>2,
若k≤2,则g'(x)>0,即g(x)在(0,+∞)上递增,
∴g(x)>g(0)即g(x)>1>0,
∴(x+1)[1+ln(x+1)]>kx(k∈N*)在(0,+∞)上恒成立;
若k>2则g(x)不为单调函数.
故k的最大值为2.
函数f(x)的导数f'(x)=-2x+
| 1 |
| x+1 |
令f'(x)>0则
| 1 |
| x+1 |
解得
-1-
| ||
| 2 |
-1+
| ||
| 2 |
令f'(x)<0则
| 1 |
| x+1 |
解得x>
-1+
| ||
| 2 |
-1-
| ||
| 2 |
∵x>-1,
∴f(x)的单调增区间为(-1,
| ||
| 2 |
单调减区间为(
| ||
| 2 |
(Ⅱ)不等式f(x)>
| kx |
| x+1 |
即1-x2+ln(x+1)>
| kx |
| x+1 |
| kx |
| x+1 |
即(x+1)[1+ln(x+1)]>kx(k∈N*)在(0,+∞)上恒成立,
令g(x)=(x+1))[1+ln(x+1)]-kx,则
g'(x)=2+ln(x+1)-k,
∵x>0,∴2+ln(x+1)>2,
若k≤2,则g'(x)>0,即g(x)在(0,+∞)上递增,
∴g(x)>g(0)即g(x)>1>0,
∴(x+1)[1+ln(x+1)]>kx(k∈N*)在(0,+∞)上恒成立;
若k>2则g(x)不为单调函数.
故k的最大值为2.
点评:本题主要考查运用导数求函数的单调性,求解时应注意函数的定义域,同时考查含参不等式恒成立问题,通常运用参数分离,转化为求函数的最值,但求最值较难,本题转化为大于0的不等式,构造函数g(x),运用导数说明g(x)>0恒成立,从而得到结论.这种思想方法要掌握.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
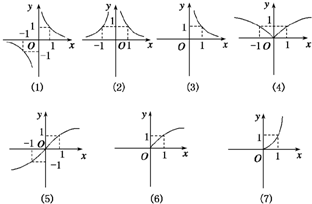
给定一组函数解析式:①y=x
;②y=x
;③y=x-
;④y=x-
;⑤y=x
;⑥y=x-
;⑦y=x
,如图所示一组函数图象.图象对应的解析式号码顺序正确的是( )
| 3 |
| 4 |
| 2 |
| 3 |
| 3 |
| 2 |
| 2 |
| 3 |
| 3 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |

| A、⑥③④②⑦①⑤ |
| B、⑥④②③⑦①⑤ |
| C、⑥④③②⑦①⑤ |
| D、⑥④③②⑦⑤① |
