题目内容
设函数f(x)=x2+aln(x+1)(a为常数)
(Ⅰ)若函数y=f(x)在区间[1,+∞)上是单凋递增函数,求实数a的取值范围;
(Ⅱ)若函数y=f(x)有两个极值点x1,x2,且x1<x2,求证:0<
<-
+ln2.
(Ⅰ)若函数y=f(x)在区间[1,+∞)上是单凋递增函数,求实数a的取值范围;
(Ⅱ)若函数y=f(x)有两个极值点x1,x2,且x1<x2,求证:0<
| f(x2) |
| x1 |
| 1 |
| 2 |
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:转化思想
分析:(Ⅰ)已知原函数的值为正,得到导函数的值非负,从而求出参量的范围;
(Ⅱ)利用韦达定理,对所求对象进行消元,得到一个新的函数,对该函数求导后,再对导函数求导,通过对导函数的导导函数的研究,得到导函数的最值,从而得到原函数的最值,即得到本题结论.
(Ⅱ)利用韦达定理,对所求对象进行消元,得到一个新的函数,对该函数求导后,再对导函数求导,通过对导函数的导导函数的研究,得到导函数的最值,从而得到原函数的最值,即得到本题结论.
解答:
解:(Ⅰ)根据题意知:f′(x)=
≥0在[1,+∞)上恒成立.
即a≥-2x2-2x在区间[1,+∞)上恒成立.
∵-2x2-2x在区间[1,+∞)上的最大值为-4,
∴a≥-4;
经检验:当a=-4时,f ′(x)=
=
≥0,x∈[1,+∞).
∴a的取值范围是[-4,+∞).
(Ⅱ)f ′(x)=
=0在区间(-1,+∞)上有两个不相等的实数根,
即方程2x2+2x+a=0在区间(-1,+∞)上有两个不相等的实数根.
记g(x)=2x2+2x+a,则有
,解得0<a<
.
∴x1+x2=-1,2x22+2x2+a=0,x2=-
+
,-
<x2<0.
∴
=
令k(x)=
,x∈(-
,0).
k′(x)=
+2ln(x+1),
记p(x)=
+2ln(x+1).
∴p′(x)=
,
p′(-
)=-4,p′(0)=2.
在x0∈(-
,0)使得p′(x0)=0.
当 x∈(-
,x0),p′(x)<0;当x∈(x0,0)时,p′(x)>0.
而k′(x)在(-
,x0)单调递减,在(x0,0)单调递增,
∵k′(-
)=1-2ln2<0.k′(0)=0,
∴当x∈(-
,0),k′(x)<0,
∴k(x)在(-
,0)单调递减,
即0<
<-
+ln2.
| 2x2+2x+a |
| x+1 |
即a≥-2x2-2x在区间[1,+∞)上恒成立.
∵-2x2-2x在区间[1,+∞)上的最大值为-4,
∴a≥-4;
经检验:当a=-4时,f ′(x)=
| 2x2+2x-4 |
| x+1 |
| 2(x+2)(x-1) |
| (x+1) |
∴a的取值范围是[-4,+∞).
(Ⅱ)f ′(x)=
| 2x2+2x+a |
| x+1 |
即方程2x2+2x+a=0在区间(-1,+∞)上有两个不相等的实数根.
记g(x)=2x2+2x+a,则有
|
| 1 |
| 2 |
∴x1+x2=-1,2x22+2x2+a=0,x2=-
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
∴
| f(x2) |
| x1 |
| x22-(2x22+2x2)ln(x2+1) |
| -1-x2 |
令k(x)=
| x2-(2x2+2x)ln(x+1) |
| -1-x |
| 1 |
| 2 |
k′(x)=
| x2 |
| (1+x)2 |
记p(x)=
| x2 |
| (1+x)2 |
∴p′(x)=
| 2x2+6x+2 |
| (1+x)3 |
p′(-
| 1 |
| 2 |
在x0∈(-
| 1 |
| 2 |
当 x∈(-
| 1 |
| 2 |
而k′(x)在(-
| 1 |
| 2 |
∵k′(-
| 1 |
| 2 |
∴当x∈(-
| 1 |
| 2 |
∴k(x)在(-
| 1 |
| 2 |
即0<
| f(x2) |
| x1 |
| 1 |
| 2 |
点评:本题考查的是导数知识,重点是利用导数法研究函数的单调性、究极值和最值,难点是多次连续求导,即二次求导,本题还用到消元的方法,难度较大.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
设集合U={x∈N*|x≤4},A={1,2},B={2,4},则(∁UA)∪B=( )
| A、{1,2} |
| B、{1,2,3,4} |
| C、{3,4} |
| D、{2,3,4} |
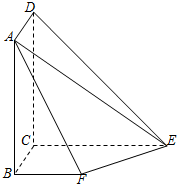 如图所示,平面ABCD⊥平面BCEF,且四边形ABCD为矩形,四边形BCEF为直角梯形,BF∥CE,BC⊥CE,DC=CE=4,BC=BF=2.
如图所示,平面ABCD⊥平面BCEF,且四边形ABCD为矩形,四边形BCEF为直角梯形,BF∥CE,BC⊥CE,DC=CE=4,BC=BF=2.