题目内容
已知圆C:x2+y2+4x-6y+8=0,直线l过定点M(-1,2).
(Ⅰ)若直线l与圆C交于不同的两点AB,且|AB|=3
,求直线l的方程;
(Ⅱ)求直线l被圆C所截弦长最短时直线l的方程以及最短长度.
(Ⅰ)若直线l与圆C交于不同的两点AB,且|AB|=3
| 2 |
(Ⅱ)求直线l被圆C所截弦长最短时直线l的方程以及最短长度.
考点:直线与圆相交的性质
专题:直线与圆
分析:(Ⅰ)将圆C化为标准方程,求出圆心和半径,根据|AB|=2=4,求出弦心距d,可得直线的斜率,再由点斜式求得直线的方程.
(Ⅱ)当直线l过点M(-1,2)且与CM垂直时弦长最短,此时kCM的值,可得kl=1,点斜式求得直线l的方程,求出弦心距,从而求得弦长.
(Ⅱ)当直线l过点M(-1,2)且与CM垂直时弦长最短,此时kCM的值,可得kl=1,点斜式求得直线l的方程,求出弦心距,从而求得弦长.
解答:
解:(Ⅰ)将圆C化为标准方程(x+2)2+(y-3)2=5,它是以C(-2,3)为圆心,
为半径的圆.
当直线l垂直x轴时,直线l的方程为x=-1,圆心到直线x=-1的距离为1,
由于|AB|=2
=4,故不合题意.
当直线l不垂直x轴时,设直线l的方程为y-2=k(x+1),即kx-y+k+2=0,圆心到直线l的距离为d,
则d=
=
=
=
,
两边平方化简得k2+4k+1=0,解得k=-2+
,或者k=-2-
,
故直线l的方程为(-2+
)x-y+
=0或(-2-
)x-y-
=0,
即 (2-
)x+y-
=0或(2+
)x+y+
=0.
(Ⅱ)当直线l过点M(-1,2)且与CM垂直时弦长最短,此时kCM=-2+13-2=-1,
则kl=1,故直线l的方程为x-y+3=0,弦心距d=
=
,弦长为2
=2
.
| 5 |
当直线l垂直x轴时,直线l的方程为x=-1,圆心到直线x=-1的距离为1,
由于|AB|=2
| 5-1 |
当直线l不垂直x轴时,设直线l的方程为y-2=k(x+1),即kx-y+k+2=0,圆心到直线l的距离为d,
则d=
| |-2k-3+k+2| | ||
|
r2-(
|
5-
|
| ||
| 2 |
两边平方化简得k2+4k+1=0,解得k=-2+
| 3 |
| 3 |
故直线l的方程为(-2+
| 3 |
| 3 |
| 3 |
| 3 |
即 (2-
| 3 |
| 3 |
| 3 |
| 3 |
(Ⅱ)当直线l过点M(-1,2)且与CM垂直时弦长最短,此时kCM=-2+13-2=-1,
则kl=1,故直线l的方程为x-y+3=0,弦心距d=
| |-2-3+3| | ||
|
| 2 |
| r2-d2 |
| 3 |
点评:本题主要考查圆的标准方程,直线和圆的位置关系,点到直线的距离公式、弦长公式的应用,属于中档题.

练习册系列答案
相关题目
已知A(-2,-2),B(4,2),点P在圆x2+y2=1上运动,则|PA|2+|PB|2的最大值是( )
| A、28 | B、30 | C、32 | D、34 |
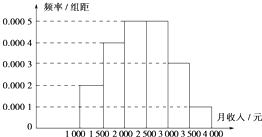 某市统计局就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500)):
某市统计局就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500)):