题目内容
函数f(x)=cos2(x-
)-cos2(x+
).
(Ⅰ)当x∈[0,
]时,求f(x)的值域;
(Ⅱ)在△ABC中,已知sinB=cosAsinC,f(B)=
,
•
=4
,求△ABC的面积.
| π |
| 6 |
| π |
| 3 |
(Ⅰ)当x∈[0,
| π |
| 2 |
(Ⅱ)在△ABC中,已知sinB=cosAsinC,f(B)=
| 1 |
| 2 |
| AB |
| AC |
| 3 |
考点:正弦定理,三角函数中的恒等变换应用
专题:综合题
分析:(Ⅰ)首先将函数f(x)进行化简,从而根据定义域确定值域.
(Ⅱ)根据已知条件求出△ABC中各角的度数,再利用向量积确定bc的值,从而求出△ABC的面积.
(Ⅱ)根据已知条件求出△ABC中各角的度数,再利用向量积确定bc的值,从而求出△ABC的面积.
解答:
解:(Ⅰ)f(x)=cos2(x-
)-cos2(x+
)
=cos2(x-
)-sin2[
-(x+
)]
=cos2(x-
)-sin2(x-
)
=cos(2x-
).
由x∈[0,
],得2x-
∈[-
,
]
∴f(x)的值域为[-
,1].
(Ⅱ)∵sinB=cosAsinC
∴cosAsinC=sin(A+C)=sinAcosC+cosAsinC
∴sinAcosC=0,
∴C=90°.
f(B)=cos(2B-
)=
,-
<2B<
.
则2B-
=
.
∴B=
,A=
.
又∵
•
=cbcosA=
bc=4
.
∴bc=8.
∴S△ABC=
cbsinA=
×8×
=2.
| π |
| 6 |
| π |
| 3 |
=cos2(x-
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
=cos2(x-
| π |
| 6 |
| π |
| 6 |
=cos(2x-
| π |
| 3 |
由x∈[0,
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
∴f(x)的值域为[-
| 1 |
| 2 |
(Ⅱ)∵sinB=cosAsinC
∴cosAsinC=sin(A+C)=sinAcosC+cosAsinC
∴sinAcosC=0,
∴C=90°.
f(B)=cos(2B-
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| 2π |
| 3 |
则2B-
| π |
| 3 |
| π |
| 3 |
∴B=
| π |
| 3 |
| π |
| 6 |
又∵
| AB |
| AC |
| ||
| 2 |
| 3 |
∴bc=8.
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查三角函数化简,正弦定理已经向量的综合知识,属于中档题.

练习册系列答案
相关题目
已知A={0,1},B={x|x⊆A},则A与B的关系正确的是( )
| A、A⊆B | B、A∈B |
| C、B?A | D、B⊆A |
不等式(x-2)(2x+1)>0的解集是( )
A、(-
| ||
B、(-2,
| ||
C、(-∞,-2)∪(
| ||
D、(-∞,-
|
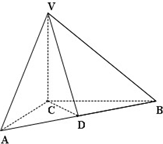 如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D为AB的中点,且AC=BC=VC=a.
如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D为AB的中点,且AC=BC=VC=a.