题目内容
已知平面内两点A(8,-6),B(2,2).
(Ⅰ)求AB的中垂线方程;
(Ⅱ)求过P(2,-3)点且与直线AB平行的直线l的方程;
(Ⅲ)一束光线从B点射向(Ⅱ)中的直线l,若反射光线过点A,求反射光线所在的直线方程.
(Ⅰ)求AB的中垂线方程;
(Ⅱ)求过P(2,-3)点且与直线AB平行的直线l的方程;
(Ⅲ)一束光线从B点射向(Ⅱ)中的直线l,若反射光线过点A,求反射光线所在的直线方程.
考点:与直线关于点、直线对称的直线方程,直线的一般式方程与直线的垂直关系
专题:直线与圆
分析:(I)先由中点坐标公式求出中点坐标,然后根据垂直求出中垂线的斜率,进而由点斜式求出直线方程;
(II)根据平行得出斜率,从而由点斜式求出直线方程;
(III)求得点B关于直线l的对称点B'的坐标,然后求出斜率,再由点斜式求出直线方程即可.
(II)根据平行得出斜率,从而由点斜式求出直线方程;
(III)求得点B关于直线l的对称点B'的坐标,然后求出斜率,再由点斜式求出直线方程即可.
解答:
解:(Ⅰ)
=5,
=-2,∴AB的中点坐标为(5,-2)----------------------(1分)
kAB=
=-
,
∴AB的中垂线斜率为
----------------------------(2分)
∴由点斜式可得y+2=
(x-5)------------------------------(3分)
∴AB的中垂线方程为3x-4y-23=0------------------------------(4分)
(Ⅱ)由点斜式y+3=-
(x-2)---------------------------------(5分)
∴直线l的方程4x+3y+1=0---------------------------------(6分)
(Ⅲ)设B(2,2)关于直线l的对称点B'(m,n)---------------------------------(7分)
∴
,---------------------------------(8分)
解得
---------------------------------(10分)
∴B′(-
,-
),kB′A=
=-
---------------------------------(11分)
由点斜式可得y+6=-
(x-8),整理得11x+27y+74=0
∴反射光线所在的直线方程为11x+27y+74=0.---------------------------------(12分)
| 8+2 |
| 2 |
| -6+2 |
| 2 |
kAB=
| -6-2 |
| 8-2 |
| 4 |
| 3 |
∴AB的中垂线斜率为
| 3 |
| 4 |
∴由点斜式可得y+2=
| 3 |
| 4 |
∴AB的中垂线方程为3x-4y-23=0------------------------------(4分)
(Ⅱ)由点斜式y+3=-
| 4 |
| 3 |
∴直线l的方程4x+3y+1=0---------------------------------(6分)
(Ⅲ)设B(2,2)关于直线l的对称点B'(m,n)---------------------------------(7分)
∴
|
解得
|
∴B′(-
| 14 |
| 5 |
| 8 |
| 5 |
-6+
| ||
8+
|
| 11 |
| 27 |
由点斜式可得y+6=-
| 11 |
| 27 |
∴反射光线所在的直线方程为11x+27y+74=0.---------------------------------(12分)
点评:本题主要考查求一个点关于直线的对称点的坐标,用点斜式求直线的方程,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f(x)=2asin(2x+
)+b的定义域为[0,
],值域为[-5,1],则函数g(x)=abx+7在[b,a]上,( )
| π |
| 6 |
| π |
| 2 |
| A、有最大值2 |
| B、有最小值2 |
| C、有最大值1 |
| D、有最小值1 |
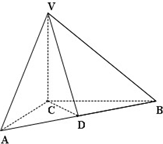 如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D为AB的中点,且AC=BC=VC=a.
如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D为AB的中点,且AC=BC=VC=a.