题目内容
y=sinx，x∈[-π，
]的单调区间 ．
| π |
| 6 |
考点：正弦函数的单调性
专题：三角函数的图像与性质
分析：结合函数y=sinx，x∈[-π，
]的图象，可得函数y的增区间．
| π |
| 6 |
解答：
解：结合函数y=sinx，x∈[-π，
]的图象，
可得y=sinx，x∈[-π，
]的单调区间为[-
，
]，
故答案为：[-
，
]．
解：结合函数y=sinx，x∈[-π，| π |
| 6 |
可得y=sinx，x∈[-π，
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
故答案为：[-
| π |
| 2 |
| π |
| 6 |
点评：本题主要考查正弦函数的单调性，属于基础题．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
将函数y=cos（x+
）的图象上各点的横坐标伸长到原来的2倍（纵坐标不变），再向左平移
个单位，所得函数图象的一个对称中心为（ ）
| π |
| 3 |
| π |
| 3 |
| A、（0，0） | ||
B、（
| ||
C、（
| ||
| D、（π，0） |
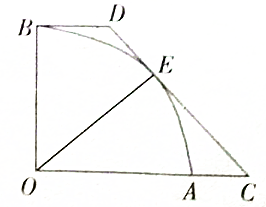如图，扇形AOB的半径OA=2，∠AOB=