题目内容
已知等比数列{an}的通项公式为an=3n-1,设数列{bn}满足对任意自然数n都有
+
+
+…+
=2n+1恒成立.
①求数列{bn}的通项公式;
②求b1+b2+b3+…+b2005的值.
| b1 |
| a1 |
| b2 |
| a2 |
| b3 |
| a3 |
| bn |
| an |
①求数列{bn}的通项公式;
②求b1+b2+b3+…+b2005的值.
考点:数列递推式,数列的求和
专题:点列、递归数列与数学归纳法
分析:本题①利用数列前n项和与通项的关系,得到
的表达式,再利用数列{an}的通项公式为an=3n-1,求出数列{bn}的通项公式;
②由①知数列{bn}的通项公式,利用等比数列求和公式,求出b1+b2+b3+…+b2005的值,得到本题结论.
| bn |
| an |
②由①知数列{bn}的通项公式,利用等比数列求和公式,求出b1+b2+b3+…+b2005的值,得到本题结论.
解答:
解:①∵对任意自然数n都有
+
+
+…+
=2n+1恒成立,
∴当n=1时,
=3,
∵等比数列{an}的通项公式为an=3n-1,
∴b1=3a1=3.
当n≥2,n∈N*时,
+
+…+
=2n-1,
∴
=2,
∵等比数列{an}的通项公式为an=3n-1,
∴bn=2×3n-1,n≥2,n∈N*.
∴bn=
.
②记S=b1+b2+b3+…+b2005,
由①知:bn=
,
∴S=3+2×3+2×32+2×33+…+2×32004
=3+
=3×22004.
∴b1+b2+b3+…+b2005=3×22004.
| b1 |
| a1 |
| b2 |
| a2 |
| b3 |
| a3 |
| bn |
| an |
∴当n=1时,
| b1 |
| a1 |
∵等比数列{an}的通项公式为an=3n-1,
∴b1=3a1=3.
当n≥2,n∈N*时,
| b1 |
| a1 |
| b2 |
| a2 |
| bn-1 |
| an-1 |
∴
| bn |
| an |
∵等比数列{an}的通项公式为an=3n-1,
∴bn=2×3n-1,n≥2,n∈N*.
∴bn=
|
②记S=b1+b2+b3+…+b2005,
由①知:bn=
|
∴S=3+2×3+2×32+2×33+…+2×32004
=3+
| 6(1-32004) |
| 1-3 |
=3×22004.
∴b1+b2+b3+…+b2005=3×22004.
点评:本题考查了数列的前n项和与数列通项的关系,还考查了等比数列的求和公式、分类讨论的数学思想,本题难度适中,计算量不大,属于中档题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
将函数y=cos(x+
)的图象上各点的横坐标伸长到原来的2倍(纵坐标不变),再向左平移
个单位,所得函数图象的一个对称中心为( )
| π |
| 3 |
| π |
| 3 |
| A、(0,0) | ||
B、(
| ||
C、(
| ||
| D、(π,0) |

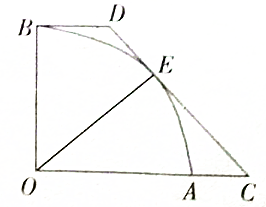 如图,扇形AOB的半径OA=2,∠AOB=
如图,扇形AOB的半径OA=2,∠AOB=