题目内容
设函数f（x）=x|x-a|，若对?x1，x2∈[3，+∞），x1≠x2，不等式
＞0恒成立，则实数a的取值范围是（ ）
| f(x1)-f(x2) |
| x1-x2 |
| A、（-∞，-3] |
| B、[-3，0） |
| C、（-∞，3] |
| D、（0，3] |
考点：函数恒成立问题
专题：分类讨论,函数的性质及应用,不等式的解法及应用
分析：由条件可得 函数f（x）=x|x-a|在[3，+∞）上是增函数，对a讨论，当a≤3时，当a＞3时，求得单调区间，即可得到a≤3．
解答：
解：∵对于任意x1，x2∈[3，+∞），x1≠x2，不等式
＞0恒成立，
∴函数f（x）=x|x-a|在[3，+∞）上是增函数．
由函数f（x）=x|x-a|=
，
当a≤3时，f（x）=x2-ax（x≥3）在（
，+∞）递增，则在[3，+∞）递增；
当a＞3时，f（x）的增区间为（a，+∞），减区间为（-∞，a），即有f（x）在[3，+∞）先减后增．
综上可得，a≤3，
故实数a的取值范围是（-∞，3]．
故选C．
| f(x1)-f(x2) |
| x1-x2 |
∴函数f（x）=x|x-a|在[3，+∞）上是增函数．
由函数f（x）=x|x-a|=
|
当a≤3时，f（x）=x2-ax（x≥3）在（
| a |
| 2 |
当a＞3时，f（x）的增区间为（a，+∞），减区间为（-∞，a），即有f（x）在[3，+∞）先减后增．
综上可得，a≤3，
故实数a的取值范围是（-∞，3]．
故选C．
点评：本题主要考查函数的单调性的判断和证明，函数的单调性的应用，掌握分类讨论的思想方法和两区间的包含关系是解题的关键，属于中档题．
练习册系列答案
相关题目
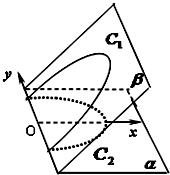如右图二面角α-y-β的大小为60°，平面β上的曲线C1在平面α上的正射影为曲线C2，C2在直角坐标系xOy下的方程x2+y2=1（0≤x≤1），则曲线C1的离心率（ ）| A、e=1 | ||||
| B、e＞1 | ||||
C、e=
| ||||
D、e=
|
