题目内容
已知函数f(x)=2sin(2x+
)+a+1(a∈R,a为常数).
(1)若x∈R,求f(x)的最小正周期;
(2)若f(x)在[-
,
]上最大值与最小值之和为3,求a的值.
| π |
| 6 |
(1)若x∈R,求f(x)的最小正周期;
(2)若f(x)在[-
| π |
| 6 |
| π |
| 6 |
考点:正弦函数的图象,三角函数的周期性及其求法
专题:三角函数的图像与性质
分析:(1)若x∈R,根据函数的周期公式即可求f(x)的最小正周期;
(2)若f(x)在[-
,
]上最大值与最小值之和为3,求出函数的最值建立方程关系即可求a的值.
(2)若f(x)在[-
| π |
| 6 |
| π |
| 6 |
解答:
解:(1)若x∈R,则f(x)的最小正周期T=
=π;
(2)若x∈[-
,
],
则2x+
∈[-
,
],
若f(x)在[-
,
]上最大值与最小值之和为3,
则函数的最大值为2sin
+a+1=a+3,
最小值为2sin(-
)+a+1=a,
则a+3+a=3,解得a=0.
| 2π |
| 2 |
(2)若x∈[-
| π |
| 6 |
| π |
| 6 |
则2x+
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
若f(x)在[-
| π |
| 6 |
| π |
| 6 |
则函数的最大值为2sin
| π |
| 2 |
最小值为2sin(-
| π |
| 6 |
则a+3+a=3,解得a=0.
点评:本题主要考查三角函数的周期的计算以及函数的最值的应用,要求熟练掌握三角函数的性质.

练习册系列答案
相关题目
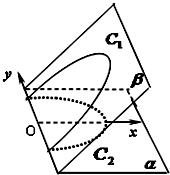 如右图二面角α-y-β的大小为60°,平面β上的曲线C1在平面α上的正射影为曲线C2,C2在直角坐标系xOy下的方程x2+y2=1(0≤x≤1),则曲线C1的离心率( )
如右图二面角α-y-β的大小为60°,平面β上的曲线C1在平面α上的正射影为曲线C2,C2在直角坐标系xOy下的方程x2+y2=1(0≤x≤1),则曲线C1的离心率( )| A、e=1 | ||||
| B、e>1 | ||||
C、e=
| ||||
D、e=
|
若全集U=R,集合A={x|x2+x-2≤0},B={y|y=log2(x+3),x∈A},则集合A∩(∁UB)=( )
| A、{x|-2≤x<0} |
| B、{x|0≤x≤1} |
| C、{x|-3<x≤-2} |
| D、{x|x≤-3} |