题目内容
19.在△ABC中,D,E分别为线段AB,AC上的点,且$AD=\frac{1}{2}AB$,$AE=\frac{2}{3}AC$,若BE⊥CD,则sinA的最大值为$\frac{1}{2}$.分析 以A为原点,以AC所在的直线为x轴,建立如图所示的直角坐标系,设△ABC中的边BC,AC,AB,分别为a,b,c,可得D($\frac{1}{2}$ccosA,$\frac{1}{2}$csinA),E($\frac{2}{3}$b,0),$\overrightarrow{BE}$=($\frac{2}{3}$b-ccosA,-csinA),$\overrightarrow{CD}$=($\frac{1}{2}$ccosA-b,$\frac{1}{2}$csinA),由$\overrightarrow{BE}$•$\overrightarrow{CD}$=($\frac{2}{3}$b-ccosA)•($\frac{1}{2}$ccosA-b)-$\frac{1}{2}$c2sin2A=0,得$\frac{4}{3}$bccosA-$\frac{2}{3}{b}^{2}$-$\frac{1}{2}$c2(cos2A+sin2A)=0,cosA=$\frac{\frac{1}{2}{c}^{2}+\frac{2}{3}{b}^{2}}{\frac{4}{3}bc}$$≥\frac{2\sqrt{\frac{1}{3}}}{\frac{4}{3}bc}bc$=$\frac{\sqrt{3}}{2}$,即可求解
解答 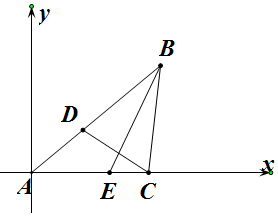 解:以A为原点,以AC所在的直线为x轴,建立如图所示的直角坐标系,
解:以A为原点,以AC所在的直线为x轴,建立如图所示的直角坐标系,
设△ABC中的边BC,AC,AB,分别为a,b,c,
∴A(0,0),C(b,0),B(ccosA,csinA),
∵$AD=\frac{1}{2}AB$,$AE=\frac{2}{3}AC$,
∴D($\frac{1}{2}$ccosA,$\frac{1}{2}$csinA),E($\frac{2}{3}$b,0),
∴$\overrightarrow{BE}$=($\frac{2}{3}$b-ccosA,-csinA),$\overrightarrow{CD}$=($\frac{1}{2}$ccosA-b,$\frac{1}{2}$csinA),
∵BE⊥CD,
∴$\overrightarrow{BE}$•$\overrightarrow{CD}$=($\frac{2}{3}$b-ccosA)•($\frac{1}{2}$ccosA-b)-$\frac{1}{2}$c2sin2A=0,
∴$\frac{4}{3}$bccosA-$\frac{2}{3}{b}^{2}$-$\frac{1}{2}$c2(cos2A+sin2A)=0,
∴cosA=$\frac{\frac{1}{2}{c}^{2}+\frac{2}{3}{b}^{2}}{\frac{4}{3}bc}$$≥\frac{2\sqrt{\frac{1}{3}}}{\frac{4}{3}bc}bc$=$\frac{\sqrt{3}}{2}$,
∴$sinA≤\sqrt{1-\frac{3}{4}}=\frac{1}{2}$,
则sinA的最大值为$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题考查了向量与三角的综合应用,考查了建立坐标系处理平面几何问题的解题策略,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
| A. | 18 | B. | 27 | C. | 36 | D. | 54 |
| A. | a≥-2 | B. | a<-2 | C. | a≤-2 | D. | a>-2 |
| A. | -cos1 | B. | cos1 | C. | |cos2| | D. | sin2 |
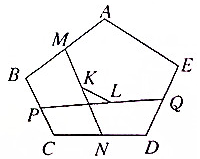 如图所示,五边形ABC 中,点M、N、P、Q分别是AB、CD、BC、DE的中点,K和L分别是MN和PQ的中点.求证:$\overrightarrow{KL}$=$\frac{1}{4}$$\overrightarrow{AE}$.
如图所示,五边形ABC 中,点M、N、P、Q分别是AB、CD、BC、DE的中点,K和L分别是MN和PQ的中点.求证:$\overrightarrow{KL}$=$\frac{1}{4}$$\overrightarrow{AE}$.